Question

PQR is a triangle right angled at P and M is a point on QR such that PM $ \bot $ QR, Show that $P{M^2} = QM \cdot MR$

Answer 1

Hint: For the right angled triangle, we have to use Pythagoras theorem to get the desired solution.

From the given information, if we draw a triangle it is similar to the figure below.

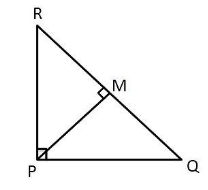
In $\vartriangle PMR,$ by Pythagoras theorem,
${\left( {PR} \right)^2} = {\left( {PM} \right)^2} + {\left( {RM} \right)^2}$ .... (1)
In $\vartriangle PMQ,$by Pythagoras theorem,
${\left( {PQ} \right)^2} = {\left( {PM} \right)^2} + {\left( {MQ} \right)^2}$ .... (2)
In $\vartriangle PQR,$ by Pythagoras theorem,
${\left( {RQ} \right)^2} = {\left( {RP} \right)^2} + {\left( {PQ} \right)^2}$ .... (3)
$\therefore {\left( {RM + MQ} \right)^2} = {\left( {RP} \right)^2} + {\left( {PQ} \right)^2}$
$\therefore {\left( {RM + MQ} \right)^2} + 2RM \cdot MQ = {(RP)^2} + {(PQ)^2}$ .... (4)
Adding equation (1) and (2) we get,
${\left( {PR} \right)^2} + {\left( {PQ} \right)^2} = 2{\left( {PM} \right)^2} + {\left( {RM} \right)^2} + {\left( {MQ} \right)^2}$ .... (5)
From equations (4) and (5), we get
$2RM \cdot MQ = 2{\left( {PM} \right)^2}$
$\therefore {\left( {PM} \right)^2} = RM.MQ$
Hence proved.
Note:If a perpendicular is drawn from the vertex of the right angle to the hypotenuse then triangles on both sides of the perpendicular are similar to the whole triangle and to each other. If two triangles are similar, then the ratio of their corresponding sides are equal.