Question

Prove by vector method:
$\cos \left( {A + B} \right) = \cos A\cos B - \sin A\sin B$

Answer 1

Hint: Here, we will first draw a figure showing two unit vectors with one of the angles negative i.e. below the $x$ axis. Hence, using the dot-product with vector form and the Cartesian form, after drawing the figure, we will be able to equate both the dot-products. Hence, we will be able to prove the given trigonometric identity.

Complete step by step solution:
In order to prove the given trigonometric identity using vector method, we will, first of all, let $OP$ and $OQ$ be two unit vectors such that they are making the angles $A$ and $B$ respectively with the positive direction of $x$ axis but above and below the axis respectively.
Hence, we have the figure:

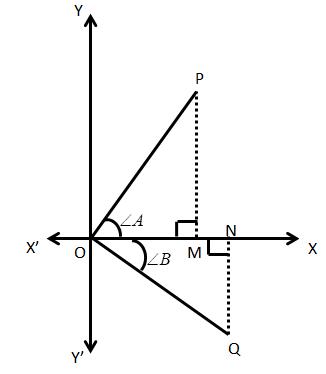
Hence, clearly from the figure, $\angle QOP = \angle A + B$
Now, we know that,
$\widehat {OP} = \overrightarrow {OM} + \overrightarrow {MP} $
$ \Rightarrow \widehat {OP} = \widehat i\cos A + \widehat j\sin A$
Similarly,
$\widehat {OQ} = \overrightarrow {ON} + \overrightarrow {NQ} $
$ \Rightarrow \widehat {OQ} = \widehat i\cos B - \widehat j\sin B$
Now, by using dot-product,
$\widehat {OP} \cdot \widehat {OQ} = \left| {OP} \right|\left| {OQ} \right|\cos \left( {A + B} \right)$
And since, these are unit vectors, thus, we get,
$\widehat {OP} \cdot \widehat {OQ} = 1 \times \cos \left( {A + B} \right) = \cos \left( {A + B} \right)$……………………….$\left( 1 \right)$
Also, in terms of components, we have,
$\widehat {OP} \cdot \widehat {OQ} = \left( {\widehat i\cos A + \widehat j\sin A} \right)\left( {\widehat i\cos B - \widehat j\sin B} \right)$
Solving this further, we get,
$\widehat {OP} \cdot \widehat {OQ} = \cos A\cos B - \sin A\sin B$………………………….$\left( 2 \right)$
Hence, equating $\left( 1 \right)$ and $\left( 2 \right)$, we get,
$\cos \left( {A + B} \right) = \cos A\cos B - \sin A\sin B$
Therefore, this is the required answer.
Hence, proved

Note:
A scalar is a quantity that has a magnitude whereas; a vector is a mathematical quantity that has both magnitude and direction. A line of given length and pointing along a given direction, such as an arrow, is a typical representation of a vector. Now, position vector is also known as location vector, it is a straight line having one end fixed and the other end attached to a moving point, it is used to describe the position of a certain point, which turns out to be its respective coordinates.