Question

Prove that $\arcsin \left( -x \right)=-\arcsin x,x\in \left[ -1,1 \right]$

Answer 1

Hint: Use the fact that if $y=\arcsin x$, then $x=\sin y$. Assume y =arscsin(-x). Use the previously mentioned fact and write x in terms of y. Use the fact that sinx is an odd function. Finally, take inverse again and hence use the fact that if $y\in \left[ -\dfrac{\pi }{2},\dfrac{\pi }{2} \right]$, then $\arcsin \left( \sin y \right)=y$ and hence prove the result.

Complete Step-by-step answer:
Before dwelling into the proof of the above question, we must understand how ${{\sin }^{-1}}x$ is defined even when $\sin x$ is not one-one.
We know that sinx is a periodic function.
Let us draw the graph of sinx

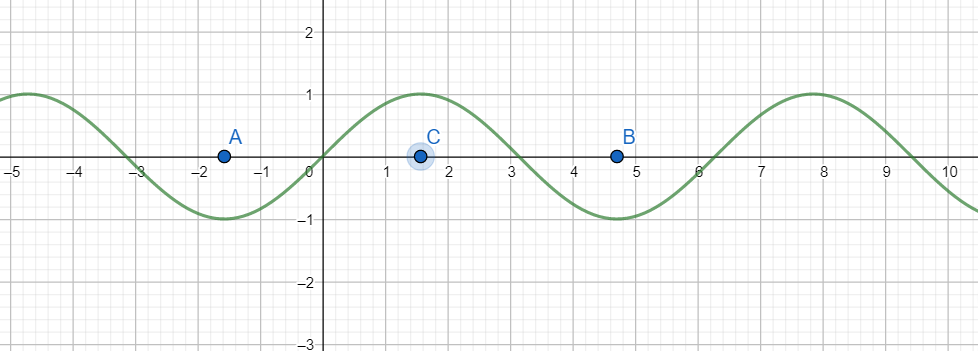
As is evident from the graph sinx is a repeated chunk of the graph of sinx within the interval $\left[ A,B \right]$ , and it attains all its possible values in the interval $\left[ A,C \right]$. Here $A=\dfrac{-\pi }{2},B=\dfrac{3\pi }{2}$ and $C=\dfrac{\pi }{2}$
Hence if we consider sinx in the interval [A, C], we will lose no value attained by sinx, and at the same time, sinx will be one-one and onto.
Hence $\arcsin x$ is defined over the domain $\left[ -1,1 \right]$, with codomain $\left[ \dfrac{-\pi }{2},\dfrac{\pi }{2} \right]$ as in the domain $\left[ \dfrac{-\pi }{2},\dfrac{\pi }{2} \right]$, sinx is one-one and ${{R}_{\sin x}}=\left[ -1,1 \right]$.
Now since $\arcsin x$ is the inverse of sinx it satisfies the fact that if $y=\arcsin x$, then $\sin y=x$.
So let y = arcsin(-x), $y\in \left[ -\dfrac{\pi }{2},\dfrac{\pi }{2} \right]$
Hence we have siny =- x.
Hence we have $x=-\sin y$
Now since sinx is an odd function, we have $x=\sin \left( -y \right)$
Taking arcsin on both sides, we get
$\arcsin x=\arcsin \left( \sin \left( -y \right) \right)$
Now since $y\in \left[ -\dfrac{\pi }{2},\dfrac{\pi }{2} \right]$, we have $-y\in \left[ -\dfrac{\pi }{2},\dfrac{\pi }{2} \right]$
We know that if $y\in \left[ -\dfrac{\pi }{2},\dfrac{\pi }{2} \right]$, then $\arcsin \left( \sin y \right)=y$ [Valid only in principal branch]
Hence we have
$\begin{align}
  & \arcsin x=-y \\
 & \Rightarrow y=-\arcsin x \\
\end{align}$
Reverting to the original variable, we get
$\arcsin \left( -x \right)=-\arcsin x$
Since -x is in the domain of $\arcsin $, we get
$-x\in \left[ -1,1 \right]\Rightarrow x\in \left[ -1,1 \right]$
Hence we have $\arcsin \left( -x \right)=-\arcsin \left( x \right),x\in \left[ -1,1 \right]$

Note: [1] The above-specified codomain for arcsinx is called principal branch for arcsinx. We can select any branch as long as $\sin x$ is one-one and onto and Range $=\left[ -1,1 \right]$. Like instead of $\left[ -\dfrac{\pi }{2},\dfrac{\pi }{2} \right]$, we can select the interval $\left[ \dfrac{\pi }{2},\dfrac{3\pi }{2} \right]$. The above formula is valid only in the principal branch.