Question

Prove that in an isosceles trapezoid, adjacent angles at the parallel sides are equal?

Answer 1

Hint: A trapezium is a cyclic quadrilateral with one pair of parallel sides. An isosceles trapezoid has one pair of parallel sides and another pair of congruent sides (means equal in length). The diagonals are of equal length in isosceles trapezoids. Using these properties, we will prove that the adjacent angles at the parallel sides are equal.

Complete solution:
          

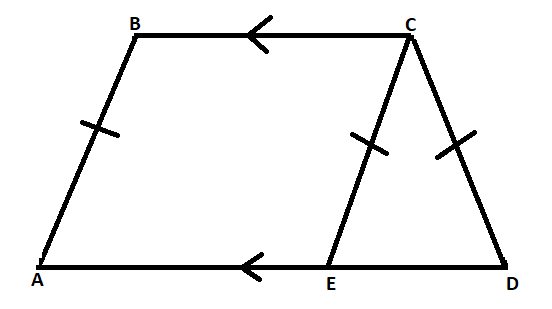
Let us consider the isosceles trapezoid $ABCD$ where $BC//AD$ and $AB = CD$ as shown below, in which we have drawn $CE//AB$.
As $CE//AB$ , we have $\angle BAE = \angle CED$.
As $CE//AB$ and $AE//BC$, $ABCE$ is a parallelogram and hence $AB = CE$ and, but as $AB = CD$, we have $CD = CE$.
Therefore, $\vartriangle CDE$ is an isosceles triangle and hence $\angle CED = \angle CDE$.
But as $\angle BAE = \angle CED$, we have $\angle BAE = \angle CDE$ or $\angle BAD = \angle ADC$.
Therefore, $\angle BAD$ is equals to $\angle ADC$.
Now, we know that two angles are supplementary if their sum is $180$ degrees.
Further as $AD//BC$, $\angle ABC$is supplementary to $\angle BAD$ and similarly $\angle ADC$ and $\angle BCD$ are supplementary.
As $\angle ABC$ and $\angle BCD$ are supplementary of equal angles, they too are equal.

Therefore, $\angle ABC$ and $\angle BCD$ are also equal.


Note:
An isosceles trapezoid can be defined as a trapezoid in which non-parallel sides and base angles are of the same measure. In other words, if two opposite sides (bases) of the trapezoid are parallel, and the two non-parallel sides are of equal lengths, then it is an isosceles trapezoid. To find the area of the isosceles trapezoid we have to add the base sides or parallel sides and divide it by $2$ and then multiply the result with height.