Question

Prove that the area of an equilateral triangle described on one side of the square is equal to half the area of the equilateral triangle described on one of its diagonal.

Answer 1

Hint: In the above question, a triangle with all sides equal and angles equal is an equilateral triangle and two equilateral triangles are always similar. the length of side of square is a then the length of diagonal is $\sqrt{2}a.$

Complete step-by-step answer:

Let us analyze the above question through a diagram-

.


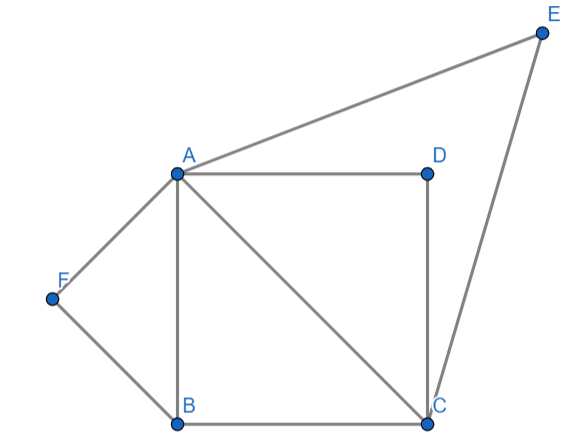Here ABCD is a square and $\vartriangle AEC$ and $\vartriangle AFB$ are two equilateral triangles described on diagonal and side of a square respectively.
We have to prove that the area of an equilateral triangle described on one side of the square is equal to half the area of the equilateral triangle described on one of it’s diagonal.
That means, $\dfrac{Area(\vartriangle AFB)}{Area(\vartriangle AEC)}=\dfrac{1}{2}$.
We know that two equilateral triangles are similar.
So, In $\vartriangle AEC$ and $\vartriangle AFB$, by SSS congruency.
$\dfrac{AE}{AF}=\dfrac{EC}{FB}=\dfrac{CA}{BA}$
We know that area of an equilateral triangle is $\dfrac{\sqrt{3}}{4}{{a}^{2}}$.
In $\vartriangle AEC$, the area of triangle can be expressed as $\dfrac{\sqrt{3}}{4}{{(AE)}^{2}},\dfrac{\sqrt{3}}{4}{{(EC)}^{2}},\dfrac{\sqrt{3}}{4}{{(CA)}^{2}}$.
and in $\vartriangle AFB$, the area of triangle can be expressed as $\dfrac{\sqrt{3}}{4}{{(BF)}^{2}},\dfrac{\sqrt{3}}{4}{{(AF)}^{2}},\dfrac{\sqrt{3}}{4}{{(AB)}^{2}}$ .
For now we will consider area of $\vartriangle AEC$ is $\dfrac{\sqrt{3}}{4}{{(AE)}^{2}}$ and the area of $\vartriangle AFB$ is $\dfrac{\sqrt{3}}{4}{{(BF)}^{2}}$.
Now, $\dfrac{Area(\vartriangle AFB)}{Area(\vartriangle AEC)}=\dfrac{\left( \dfrac{\sqrt{3}}{4}{{(AE)}^{2}} \right)}{\left( \dfrac{\sqrt{3}}{4}{{(BF)}^{2}} \right)}=\dfrac{A{{E}^{2}}}{B{{F}^{2}}}\cdot \cdot \cdot \cdot \cdot (1)$
If the length of the side of the square is ‘a’. Then by pythagoras theorem length of diagonal of square=$\sqrt{{{a}^{2}}+{{a}^{2}}}=\sqrt{2{{a}^{2}}}=\sqrt{2}a$.
The length of side AE is ‘a’ as the $\vartriangle AFB$ is described on the side of a square. So, AE=a and the length of side BF is $\sqrt{2}a$ because the $\vartriangle AEC$ is described on the diagonal of square. Now substituting AE=a and BF=$\sqrt{2}a$ in equation (1) we will get,
$\dfrac{Area(\vartriangle AFB)}{Area(\vartriangle AEC)}=\dfrac{A{{E}^{2}}}{B{{F}^{2}}}={{\left( \dfrac{AE}{BF} \right)}^{2}}={{\left( \dfrac{a}{\sqrt{2}a} \right)}^{2}}={{\left( \dfrac{1}{\sqrt{2}} \right)}^{2}}=\dfrac{1}{2}$.
So, we proved that $\dfrac{Area(\vartriangle AFB)}{Area(\vartriangle AEC)}=\dfrac{1}{2}$.
Hence, we proved that the area of an equilateral triangle described on one side of the square is equal to half the area of the equilateral triangle described on one of its diagonal.

Note: One must read the question properly and have to draw the diagram clearly and then we have to prove that the area of an equilateral triangle described on one side of the square is equal to half the area of the equilateral triangle described on one of its diagonal.