Question

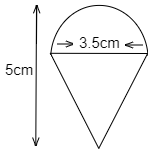
Rasheed got a playing top (lattu) as his birthday present, which surprisingly had no color on it. He wanted to color it with his crayons. The top is shaped like a cone surmounted by a hemisphere. The entire top is 5cm in height and the diameter of the top is 3.5cm. Find the area he has to color (Take $\pi =\dfrac{22}{7}$).

Answer 1

Hint: First find the radius of the top. Then, find the height of the conical part. For the area of the top, sum the lateral area of the semi-sphere and the cone. The lateral surface area of the semi-sphere is given by $2\pi {{r}^{2}}$ and of the cone is given by $\pi rl$. Substitute the values and add them to get the desired result.

Complete step by step answer:
Given: - Height of the top = 5 cm
Diameter of the top = 3.5 cm
To find: - Area Rasheed has to color.
The radius of the top is given by,
$\Rightarrow r=\dfrac{D}{2}$
Substitute the value of diameter,
$\Rightarrow r=\dfrac{3.5}{2}$
Multiply numerator and denominator by 2,
$\Rightarrow r=\dfrac{7}{4}$ cm
The height of the top is the sum of the radius of the top and the height of the cone.
$h+r=5$
Substitute the value of the radius,
$\Rightarrow h+\dfrac{7}{4}=5$
Move $\dfrac{7}{4}$ on the right side,
$\Rightarrow h=5-\dfrac{7}{4}$
Take LCM on the right side,
$\Rightarrow h=\dfrac{20-7}{4}$
Subtract the term in the numerator,
$\Rightarrow h=\dfrac{13}{7}$ cm
The slant height of the cone is given by,
$\Rightarrow l=\sqrt{{{h}^{2}}+{{r}^{2}}}$
Substitute the value of the height and radius of the cone,
$\Rightarrow l=\sqrt{{{\left( \dfrac{13}{4} \right)}^{2}}+{{\left( \dfrac{7}{4} \right)}^{2}}}$
Square the terms,
$\Rightarrow l=\sqrt{\dfrac{169}{16}+\dfrac{49}{16}}$
Add the terms inside the square root,
$\Rightarrow l=\dfrac{\sqrt{218}}{4}$cm
For the area of the top, find the lateral area of the semi-sphere and the cone.
The lateral surface area of the cone is given by,
${{A}_{C}}=\pi rl$
The lateral surface area of the hemisphere is given by,
${{A}_{S}}=2\pi {{r}^{2}}$
So, the area of the top,
$\Rightarrow A={{A}_{C}}+{{A}_{S}}$
Substitute the value,
$\Rightarrow A=\pi rl+2\pi {{r}^{2}}$
Take common on the right side,
$\Rightarrow A=\pi r\left( l+2r \right)$
Substitute the values,
$\Rightarrow A=\dfrac{22}{7}\times \dfrac{7}{4}\times \left( \dfrac{\sqrt{218}}{4}+2\times \dfrac{7}{4} \right)$
Cancel out the common factor,
$\Rightarrow A=5.5\times \left( 3.7+3.5 \right)$
Add the terms in the bracket,
$\Rightarrow A=5.5\times 7.2$
Multiply the terms,
$\Rightarrow A=39.6\text{c}{{\text{m}}^{2}}$

Hence, the area Rasheed has to color is $39.6\text{c}{{\text{m}}^{2}}$.

Note:
Hemi-sphere: A cube is a three-dimensional shape. A hemisphere is formed when the plane cuts the sphere into two halves. A sphere is a combination of the two hemispheres.
Cone: A cone is a three-dimensional shape in geometry that narrows smoothly from a flat base (usually circular base) to a point(which forms an axis to the center of the base) called the apex or vertex.