Question

What is the reference angle and what quadrant do $300$ degrees lie in?

Answer 1

Hint: Here we are going to see details about the reference angle and also the quadrant. Using this we can find the quadrant of $300$ the lie. A reference angle always uses the $x$ axis as its frame of reference. Also, we need to find whether $300$degrees lie in the first quadrant, the second quadrant, the third quadrant, or the fourth quadrant.

Complete answer:
What is the reference angle?
The reference angle is the positive acute angle that can represent an angle of any measure and the reference angle must be less than ${90^ \circ }$ . In radian measure, the reference angle must be less than $\dfrac{\pi }{2}$ .
Any angle on the $x,y$ plane has a reference angle, which is always between $0$ and $90$ degrees. The reference angle is always the smallest angle that you can make from the terminal side of an angle (that is where the angle ends) with the $x$ axis. A reference angle always uses the $x$ axis as its frame of reference.
In standard position, the angle will turn counterclockwise through the first, second, third, and into the fourth quadrant and the reference angle and the original angle together make one full circle, or ${360^ \circ }$ therefore, the reference angle is ${360^ \circ } - {300^ \circ } = {60^ \circ }$.
Quadrant:

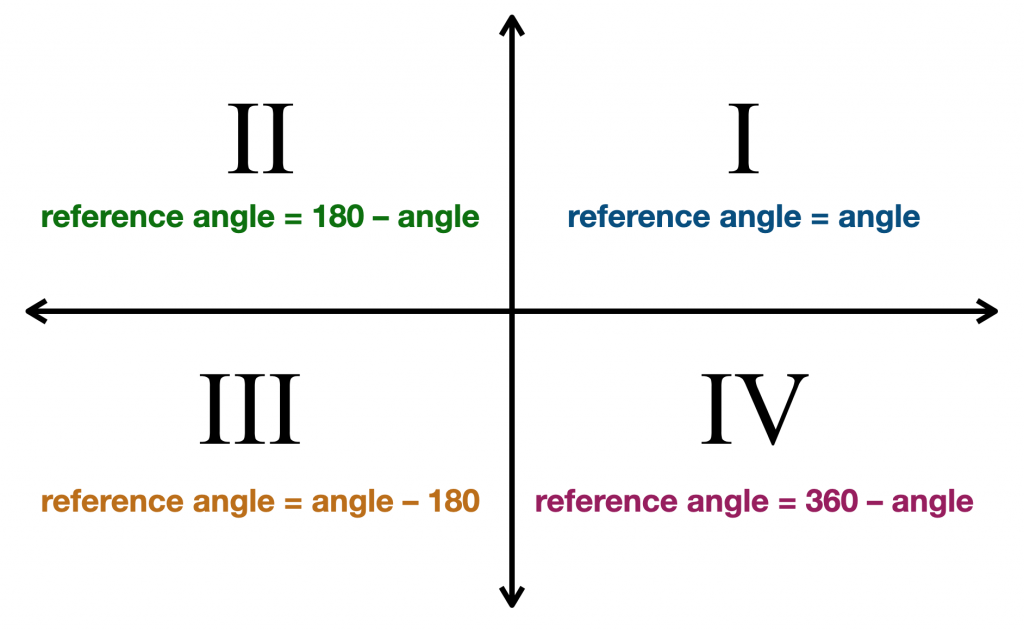
The coordinate axes divide the plane into four quadrants, namely the first quadrant, second quadrant, third quadrant, fourth quadrant.
First quadrant: Every positive angle in this quadrant is an acute angle. So the reference angle is the measure of the angle itself.
Second quadrant: In this quadrant consist of an angle between ${90^ \circ }$ to ${180^ \circ }$
Third quadrant: In this quadrant consist an angle between ${180^ \circ }$to ${270^ \circ }$
Fourth quadrant: In this quadrant consist of an angle between ${270^ \circ }$to ${360^ \circ }$
From this definition of the quadrant, $300$ degrees must lie in the fourth quadrant.

Note: Positive angles are the result of the counterclockwise rotation and negative angles are the result of the clockwise rotation.
Also, we have found that $300$ degrees must lie in the fourth quadrant