
What is the relationship between critical angle and refractive index?
Answer
514.8k+ views
Hint: Here, we will proceed by using Snell's law and then we will put the conditions for critical angle to this law and find the required relationship between critical angle and refractive index.
Complete step-by-step answer:
Formulas Used-
Let us suppose a light ray is incident from a rarer medium I having refractive index of
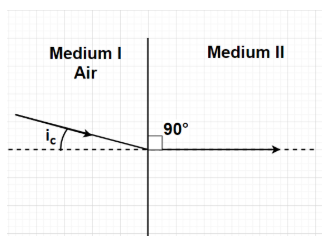
According to Snell’s law (or second law of refraction), for a light ray entering from a medium with refractive index
As the incidence angle in any medium approaches a certain critical value, the refracted ray lies along the boundary, having a refractive angle of 90 degrees. This angle of incidence is known as the critical angle. It is the highest angle of incidence for which there might still be refraction.
For critical angle (
Now, replacing i by
Using
Now, assuming the rarer medium be air which has a refractive index of 1 (i.e.,
By putting
The above equation represents the required relationship between critical angle and refractive index.
Hence, option C is correct.
Note: The refractive index is the ratio of speed of light in medium to the speed of light in vacuum. As light travels in a medium other than vacuum, the medium's atoms continually absorb and re-emit the light particles, slowing down the speed of light. Refractive index is also called a refraction index, measuring the bending of a ray of light as it travels from one medium to another.
Complete step-by-step answer:
Formulas Used-
Let us suppose a light ray is incident from a rarer medium I having refractive index of

According to Snell’s law (or second law of refraction), for a light ray entering from a medium with refractive index
As the incidence angle in any medium approaches a certain critical value, the refracted ray lies along the boundary, having a refractive angle of 90 degrees. This angle of incidence is known as the critical angle. It is the highest angle of incidence for which there might still be refraction.
For critical angle (
Now, replacing i by
Using
Now, assuming the rarer medium be air which has a refractive index of 1 (i.e.,
By putting
The above equation represents the required relationship between critical angle and refractive index.
Hence, option C is correct.
Note: The refractive index is the ratio of speed of light in medium to the speed of light in vacuum. As light travels in a medium other than vacuum, the medium's atoms continually absorb and re-emit the light particles, slowing down the speed of light. Refractive index is also called a refraction index, measuring the bending of a ray of light as it travels from one medium to another.
Recently Updated Pages
Master Class 4 Maths: Engaging Questions & Answers for Success

Master Class 4 English: Engaging Questions & Answers for Success

Master Class 4 Science: Engaging Questions & Answers for Success

Class 4 Question and Answer - Your Ultimate Solutions Guide

Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Trending doubts
Give 10 examples of unisexual and bisexual flowers

Draw a labelled sketch of the human eye class 12 physics CBSE

Differentiate between homogeneous and heterogeneous class 12 chemistry CBSE

a Tabulate the differences in the characteristics of class 12 chemistry CBSE

Why is the cell called the structural and functional class 12 biology CBSE

Differentiate between insitu conservation and exsitu class 12 biology CBSE




