Question

Represent -4, -6, 5, and 7 on the number line.

Answer 1

Hint: We draw a number line representing integers. Mark the number given in the question on the number line.
* A number line is a representation of numbers on a straight line with equal distance between consecutive numbers.
* A number line has $0$ as its center. All negative numbers lie on the left-hand side of $0$ and all positive numbers lie on the right-hand side of $0$.

Complete step by step answer:
We have to represent the numbers $-4, -6, 5$, and $7$ on the number line.
We draw a number line which represents consecutive integers at unit distance from each other. We plot a few numbers to the left-hand side of $0$ and a few numbers on to the right-hand side of $0$.

We have to represent $-4, -6, 5$, and $7$ on the number line.
We first look at the sign of the numbers
$-4$ has a negative sign
$-6$ has a negative sign
$5$ has a positive sign
$7$ has a positive sign
So, $-4$ and $-6$ lie on the left-hand side of $0,5$, and $7$ lie on the right-hand side of $0$.

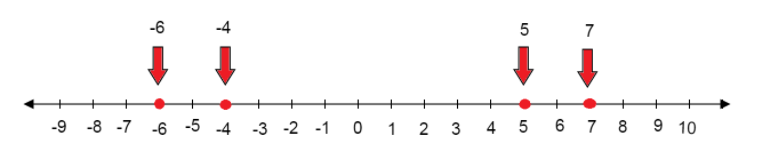
Thus, the numbers $-4, -6, 5$, and $7$ are represented on the number line.

Additional Information:
We can perform operations like addition and subtraction of numbers on the number line.
* To add numbers on the real line we move to the right side for each addition.
* To subtract numbers on the number line we move to the left side for each subtraction.
* Any number on the right-hand side of another number is always greater than that number.

Note:
While representing a number on the number line always represent the number with a different color or sign, so it is easy to locate. Also, mark a few extra numbers to the left and to the right of the number to show where the number lies.