
Represent the following data by a pie diagram:
Items of expenditure Expenditure Family A Family B Food 4000 6400 Clothing 2500 480 Rent 1500 3200 Education 400 1000 Miscellaneous 1600 600 Total 10000 11680
| Items of expenditure | Expenditure | |
| Family A | Family B | |
| Food | 4000 | 6400 |
| Clothing | 2500 | 480 |
| Rent | 1500 | 3200 |
| Education | 400 | 1000 |
| Miscellaneous | 1600 | 600 |
| Total | 10000 | 11680 |
Answer
472.2k+ views
Hint: In this question, we are given data on expenditure for two families and we have to draw a pie chart for both of them. For this, we will first change the expenditure of different items into central angles (degrees) for a circle using the formula:
\[\text{Central angle of component}=\dfrac{\text{Component Value}}{\text{Sum of all components}}\times 360\]
After that, we will make a pie chart using these degrees for both families.
Complete step-by-step solution:
Let us first change the expenditure for different items of both families into central angles. We will do it using the formula:
\[\text{Central angle of component}=\dfrac{\text{Component Value}}{\text{Sum of all components}}\times 360\]
Let us draw a table for both families and find degrees in the table.
Here, the sum of all components is 10000 for family A and 11680 for family B.
Now, let us understand the steps involved in making pie charts.
Step 1: Draw a circle of an appropriate radius.
Step 2: Draw a vertical radius of the circle drawn in step 1.
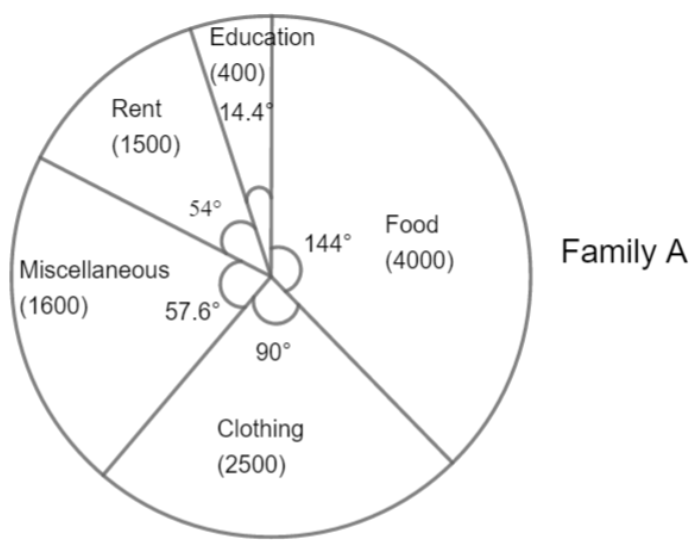
Step 3: Choose the largest central angle. Here, the largest central angle for family A is ${{144}^{\circ }}$. So, for family, A draw a sector with central angle ${{144}^{\circ }}$ in such a way that one of its radii coincide with the radius drawn in step 2 and another radius is in its counter-clockwise direction. Similarly, family B starts with ${{197.3}^{\circ }}$.
Step 4: Construct other sectors representing other items in the clockwise sense in descending order of magnitude of their central angles.
Step 5: Shade the sectors with different patterns and label them.
Now, let us draw pie charts for both families using the above steps.

Note: Students should carefully convert given data into central angles (degrees) to make pie charts. While drawing the last sector the radius should coincide with the first drawn radius. Make sure that the sum of all degrees becomes equal to ${{360}^{\circ }}$.
\[\text{Central angle of component}=\dfrac{\text{Component Value}}{\text{Sum of all components}}\times 360\]
After that, we will make a pie chart using these degrees for both families.
Complete step-by-step solution:
Let us first change the expenditure for different items of both families into central angles. We will do it using the formula:
\[\text{Central angle of component}=\dfrac{\text{Component Value}}{\text{Sum of all components}}\times 360\]
Let us draw a table for both families and find degrees in the table.
Here, the sum of all components is 10000 for family A and 11680 for family B.
| Items of expenditure | Family A | Family B | ||
| Expenditure | Sector angle | Expenditure | Sector angle | |
| Food | 4000 | $\dfrac{4000}{10000}\times 360=144$ | 6400 | $\dfrac{6400}{11680}\times 360=197.3$ |
| Clothing | 2500 | $\dfrac{2500}{10000}\times 360=90$ | 480 | $\dfrac{480}{11680}\times 360=14.8$ |
| Rent | 1500 | $\dfrac{1500}{10000}\times 360=54$ | 3200 | $\dfrac{3200}{11680}\times 360=98.6$ |
| Education | 400 | $\dfrac{1600}{10000}\times 360=57.6$ | 1000 | $\dfrac{600}{11680}\times 360=18.5$ |
| Miscellaneous | 1600 | $\dfrac{400}{10000}\times 360=14.4$ | 600 | $\dfrac{1000}{11680}\times 360=30.8$ |
Now, let us understand the steps involved in making pie charts.
Step 1: Draw a circle of an appropriate radius.
Step 2: Draw a vertical radius of the circle drawn in step 1.
Step 3: Choose the largest central angle. Here, the largest central angle for family A is ${{144}^{\circ }}$. So, for family, A draw a sector with central angle ${{144}^{\circ }}$ in such a way that one of its radii coincide with the radius drawn in step 2 and another radius is in its counter-clockwise direction. Similarly, family B starts with ${{197.3}^{\circ }}$.
Step 4: Construct other sectors representing other items in the clockwise sense in descending order of magnitude of their central angles.
Step 5: Shade the sectors with different patterns and label them.
Now, let us draw pie charts for both families using the above steps.


Note: Students should carefully convert given data into central angles (degrees) to make pie charts. While drawing the last sector the radius should coincide with the first drawn radius. Make sure that the sum of all degrees becomes equal to ${{360}^{\circ }}$.
Recently Updated Pages
What percentage of the area in India is covered by class 10 social science CBSE

The area of a 6m wide road outside a garden in all class 10 maths CBSE

What is the electric flux through a cube of side 1 class 10 physics CBSE

If one root of x2 x k 0 maybe the square of the other class 10 maths CBSE

The radius and height of a cylinder are in the ratio class 10 maths CBSE

An almirah is sold for 5400 Rs after allowing a discount class 10 maths CBSE

Trending doubts
For Frost what do fire and ice stand for Here are some class 10 english CBSE

What did the military generals do How did their attitude class 10 english CBSE

What did being free mean to Mandela as a boy and as class 10 english CBSE

What did Valli find about the bus journey How did she class 10 english CBSE

Can you say how 10th May is an Autumn day in South class 10 english CBSE

Explain the Treaty of Vienna of 1815 class 10 social science CBSE




