Question

How would you rewrite Euclid’s fifth postulate so that it would be easier to understand?

Answer 1

Hint: Here, we will proceed by firstly writing down the Euclid’s fifth postulate along with the corresponding diagram. Finally, we will be rewriting the postulate in a much simpler way by using the diagram drawn.

Complete step-by-step answer:

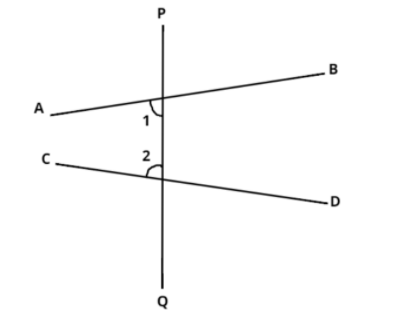
According to the Euclid’s fifth postulate, whenever a straight line falls on two different straight lines and the interior angles made on the same side of the straight line falling on two other straight lines constitutes less than two right angles then the two straight lines when produced indefinitely, meet on the side of the falling straight line where the sum of angles is less than that corresponding to two right angles.
This postulate is shown in the figure. In the figure, we can see that two straight lines AB and CD are intersected by a straight line XY. The interior angles made by the straight line XY with the straight lines AB and CD are termed as $\angle 1$ and $\angle 2$. Clearly, these interior angles made on the left side of line XY constitute less than two right angles so when the straight lines AB and CD will be produced indefinitely, they will meet on the left side to the straight line XY.
This postulate can be rewritten in reference to the above diagram as under:
Let us consider a straight line XY which falls on two straight lines AB and CD in such a way that the total sum of the interior angles $\angle 1$ and $\angle 2$ is less than 180 degrees on the left side of straight line XY. Therefore, the two straight lines AB and CD will intersect when extended on the left side of straight line XY.

Note: The Euclid’s fifth postulate also states that the perpendicular distance between any two parallel lines will always be equal when measured from different points on the two parallel lines. Also, two distinct intersecting lines can never be parallel to each other at the same time.