
Show by means of a diagram how the pattern of d-orbital changes as an octahedral complex undergoes tetragonal distortion and eventually becomes a square planar complex.
Answer
411.9k+ views
Hint :Crystal field theory: It states that the electrons donated by ligands to transition metal, then while pairing in d-orbitals, the electrons experience repulsions due to which d-subshell splits into two parts and the energy of each orbital is decided by the type of complex formed.
Complete Step By Step Answer:
According to crystal field theory, the metal is considered as the point charge and the ligands are considered as the negatively charged species which approach the metal via fixed axes. Therefore, the d-subshell of an octahedral complex experiences degeneracy and splits into two parts. The three orbitals that are
Orbitals present at the diagonals of the plane:
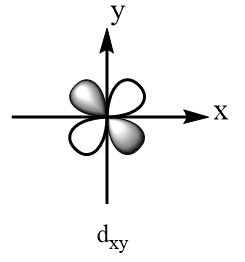
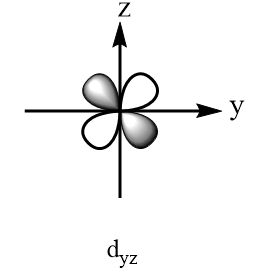
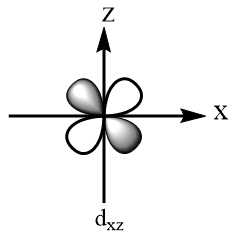
Orbitals present along the axes of the plane:
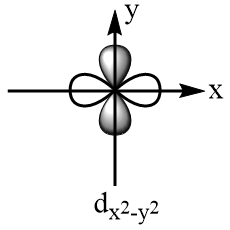
Now, to convert an octahedral complex into a square plane complex, distortion of geometry takes place via the z axis. The electrons from z axis leave the complex, so on further splitting
At the last step, when electrons of the z axis are completely removed then the
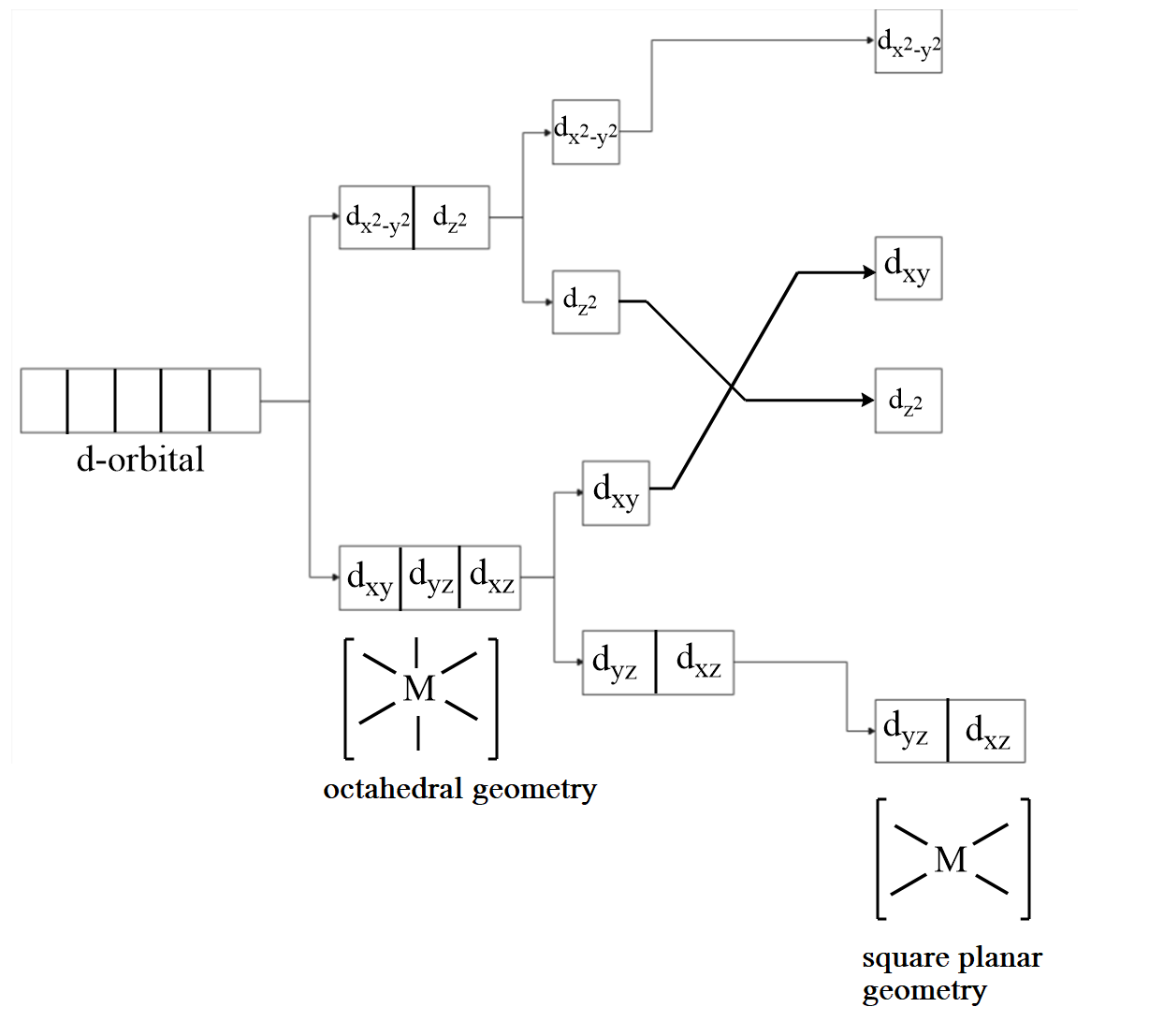
Note :
It is important to note that the difference between the energy levels obtained after splitting of orbitals is known as crystal field stabilization energy i.e., CFSE. For a complex, higher the value of CFSE, greater will be its thermodynamic stability and kinetically inert.
Complete Step By Step Answer:
According to crystal field theory, the metal is considered as the point charge and the ligands are considered as the negatively charged species which approach the metal via fixed axes. Therefore, the d-subshell of an octahedral complex experiences degeneracy and splits into two parts. The three orbitals that are
Orbitals present at the diagonals of the plane:



Orbitals present along the axes of the plane:


Now, to convert an octahedral complex into a square plane complex, distortion of geometry takes place via the z axis. The electrons from z axis leave the complex, so on further splitting
At the last step, when electrons of the z axis are completely removed then the

Note :
It is important to note that the difference between the energy levels obtained after splitting of orbitals is known as crystal field stabilization energy i.e., CFSE. For a complex, higher the value of CFSE, greater will be its thermodynamic stability and kinetically inert.
Recently Updated Pages
Master Class 4 Maths: Engaging Questions & Answers for Success

Master Class 4 English: Engaging Questions & Answers for Success

Master Class 4 Science: Engaging Questions & Answers for Success

Class 4 Question and Answer - Your Ultimate Solutions Guide

Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Trending doubts
Give 10 examples of unisexual and bisexual flowers

Draw a labelled sketch of the human eye class 12 physics CBSE

a Tabulate the differences in the characteristics of class 12 chemistry CBSE

Differentiate between homogeneous and heterogeneous class 12 chemistry CBSE

Why is the cell called the structural and functional class 12 biology CBSE

Differentiate between insitu conservation and exsitu class 12 biology CBSE




