Question

Show graphically how charge on a capacitor and current through the capacitor varies with time during charging and discharging of the capacitor.

Answer 1

Hint: To solve the given question we must have the knowledge of how the charge on a capacitor and the current through it varies with time when the capacitor is charging and discharging. Write the corresponding equations, which will make it easy to interpret the graphs.

Complete answer:
A capacitor is a device that stores charge on it when a potential difference is created across it. When the positive charge is getting deposited on the capacitor, we say that the capacitor is charging. And when the positive charge on the capacitor is decreasing, we say that capacitor is discharging. Now, consider a capacitor with capacitance C connected across a cell of emf E. Let the circuit have some resistance R. When the circuit is switched on, the capacitor gets charged gradually. The charge (q) on the capacitor at time t, when it is charging is given as $q={{q}_{0}}\left( 1-{{e}^{-\dfrac{t}{\tau }}} \right)$,
where ${{q}_{0}}$ is the maximum possible charge on the capacitor and $\tau $ is time constant.

The graph for the charge (q) on the capacitor with respect to time is as shown below:

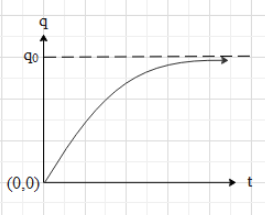
From the formula as also from the graph we can conclude that the charge on the capacitor during charging increases exponentially with respect to time. At time tending to infinity, the charge on the capacitor becomes equal to ${{q}_{0}}$ (i.e. the maximum charge).

While the capacitor is charging is charging, the current (i) through it at time t is given as $i={{i}_{0}}{{e}^{-\dfrac{t}{\tau }}}$,
where ${{i}_{0}}$ is the maximum possible current through the capacitor.
The graph for the current (i) through the capacitor with respect to time is as shown below:

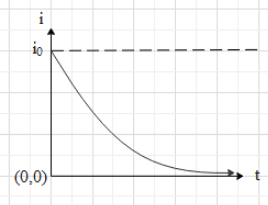
From the formula and from the graph, we conclude that when the capacitor is charging, current through it decreases exponentially with respect to time. Initially (when the circuit switched on), the current is maximum and equal to ${{i}_{0}}$. It becomes equal to zero when time tends to infinity.

Let us now see what happens to the charge and current when the capacitor is discharging.
Suppose we charge a capacitor with a cell and disconnect the cell. After the cell is disconnected, the capacitor will discharge. Let the initial charge on it is ${{q}_{0}}$ .
Then charge on the capacitor is given as $q={{q}_{0}}{{e}^{-\dfrac{t}{\tau }}}$.
The graph for the charge on a capacitor while it is discharging is given as:

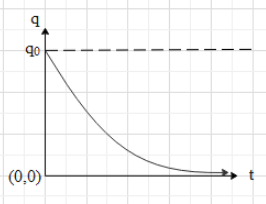
For these, we can conclude that again the charge on the capacitor is an exponential function of time. However, this time it decreases with time with a maximum value at time $t=0$.

The current through the capacitor when it is discharging is given as $i=-{{i}_{0}}{{e}^{-\dfrac{t}{\tau }}}$ …. (*).
The graph for the above is given as:

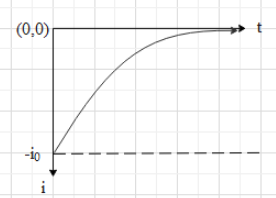
For these, we conclude that during discharging of a capacitor current (magnitude) in the circuit decreases exponentially with time.

Note: Student may misunderstand the last graph. They may think that the current is increasing in this case. It is correct that the value of current is becoming less negative with time, but note that its magnitude is decreasing. And we must only consider its magnitude. Note that the negative sign in equation (*) only shows that the capacitor is discharging.