Question

Show that a boat must move at an angle of $ 90^\circ $ with respect to river water in order to cross the river in minimum time?

Answer 1

Hint
The velocity of the river is assumed to be in the horizontal direction. Thus the crossing takes place in the vertical direction. To cross the river, the boat has to move from one edge of the river to the other, while doing this a boat may also go with the flow of water in the horizontal direction, this increases the time taken by the boat to get across the river.

Complete step by step answer
Let the direction of flow of the river be in $ {v_{river}}\hat i $ in the $ x $ direction.
Let the boat be moving with a velocity $ {v_{boat}} $ making an angle $ \theta $ with the $ x $ direction.

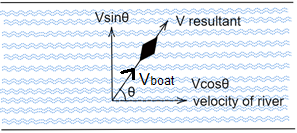
Since, velocity is defined as $ \dfrac{{ds}}{{dt}} $ ,
 $ v \propto \dfrac{1}{{dt}} $
For the time $ dt $ to be minimum, the value of $ v $ should be maximum.
The velocity of boat depends on the velocity of the river as well, so the resultant velocity is given by:
 $ {v_R} = {v_{river}}\hat i + {v_{boat}}\cos \theta \hat i + {v_{boat}}\sin \theta \hat j $
For the minimum time taken, the component of the velocity along the vertical (y axis) should be maximum.
Therefore, by using the concept of maxima and minima we should get the value of,
 $ {v_{boat}}\sin \theta = \max $
On differentiating the term and equating it to zero we get,
 $ {v_{boat}}\cos \theta = 0 $
Either $ {v_{boat}} = 0 $ or $ \operatorname{Cos} \theta = 0 $
If the velocity of the boat becomes zero, it is the minimum condition, and is not possible in this case.
Therefore for maximum velocity,
 $ \cos \theta $ should be equal to zero.
 $ \theta = \dfrac{\pi }{2}rad $ or $ 90^\circ $
Hence the time required to cross the river is minimum when the angle made by flow of river and the direction of velocity of the boat is $ 90^\circ $ .

Note
The angle $ \theta $ used here is the angle made by the resultant velocity with the direction of flow of water in the river. A boat can cross a river in minimum time If the velocity of the river is zero and the velocity of the boat is in y direction. This condition cancels out both of the terms in the x direction in the formula of the resultant velocity-
 $ {v_R} = {v_{river}}\hat i + {v_{boat}}\cos \theta \hat i + {v_{boat}}\sin \theta \hat j $
 $ {v_R} = {v_{boat}}\sin \theta \hat j $ as the angle is $ 90^\circ $ ,
 $ {v_R} = {v_{boat}} $