Question

Show that the function \[f:R \cdot \to R \cdot \] defined by \[f(x) = \dfrac{1}{x}\] is one-one and onto, where ‘\[R \cdot \]’ is the set of all non-zero real numbers. Is the result true, if the domain ‘\[R \cdot \]’ is replaced by \[N\] with a co-domain being the same as ‘\[R \cdot \]’?

Answer 1

Hint: To find whether the given function is one-one or not, we will take two elements \[{x_1}\] and \[{x_2}\] in the set of the domain of the given function and the we will substitute \[f\left( {{x_1}} \right) = f\left( {{x_2}} \right)\]. If \[{x_1} = {x_2}\], then \[f(x)\] is a one-one function. To check that the given function is onto or not, we will check if the range of \[f(x)\] is equal to the co-domain or not.

Complete step-by-step solution:
It is given that the function is defined for all non-zero real numbers and over all non-zero real numbers. Therefore, both domain and co-domain of the given function consist of the set of all non-zero real numbers.
Assume two elements \[{x_1}\] and \[{x_2}\] in the set of the domain of the given function. Therefore,
\[f\left( {{x_1}} \right) = f\left( {{x_2}} \right)\]
Substituting \[{x_1}\] and \[{x_2}\] in the function, we get
\[ \Rightarrow \dfrac{1}{{{x_1}}} = \dfrac{1}{{{x_2}}}\]
On cross multiplying, we get
\[ \Rightarrow {x_2} = {x_1}\]
On rewriting we get
\[ \Rightarrow {x_1} = {x_2}\]
Hence, we can see that, when \[f\left( {{x_1}} \right) = f\left( {{x_2}} \right)\] then \[{x_1} = {x_2}\]. Therefore, \[f\] is one-one.
Now we will check whether \[f\] is onto or not.
Given, \[f:R \cdot \to R \cdot \] where ‘\[R \cdot \]’ is the set of all non-zero real numbers defined by \[f(x) = \dfrac{1}{x}\].
Let \[y = f(x)\], such that \[y \in R \cdot \]. Therefore, we can write
\[ \Rightarrow y = \dfrac{1}{x}\]
On cross multiplying we get
\[ \Rightarrow x = \dfrac{1}{y}\]
Since, the denominator can’t be zero.
\[\therefore y \ne 0\]
Therefore, we can say that if \[y \in R - \left\{ 0 \right\}\], then \[x \in R - \left\{ 0 \right\}\] also.
Now, we will check for \[y = f(x)\].
Putting the value of \[x\] in \[f(x)\], we get
\[ \Rightarrow f(x) = f\left( {\dfrac{1}{y}} \right)\]
Substituting \[\dfrac{1}{y}\] in the function, we get
\[ \Rightarrow f(x) = \dfrac{1}{{\dfrac{1}{y}}}\]
On simplification,
\[ \Rightarrow f(x) = y\]
Thus, for every \[y \in R \cdot \], there exists \[x \in R \cdot \] such that \[f(x) = y\].
Hence, \[f\] is onto.
Now, when the domain \[R \cdot \] is replaced by \[N\] with co-domain being same as ‘\[R \cdot \]’
So, we get \[f:N \to R \cdot \]
Again, we will check if \[f:N \to R \cdot \] defined by \[f(x) = \dfrac{1}{x}\] is one-one or not.
Assume two elements \[{x_1}\] and \[{x_2}\] in the set of the domain of the given function. Therefore,
\[f\left( {{x_1}} \right) = f\left( {{x_2}} \right)\]
Substituting \[{x_1}\] and \[{x_2}\] in the function, we get
\[ \Rightarrow \dfrac{1}{{{x_1}}} = \dfrac{1}{{{x_2}}}\]
On cross multiplying, we get
\[ \Rightarrow {x_2} = {x_1}\]
On rewriting we get
\[ \Rightarrow {x_1} = {x_2}\]
Hence, we can see that, when \[f\left( {{x_1}} \right) = f\left( {{x_2}} \right)\] then \[{x_1} = {x_2}\]. Therefore, \[f\] is one-one.
Now, we will check that \[f\] is onto or not.
We have, \[f:N \to R \cdot \] defined by \[f(x) = \dfrac{1}{x}\].
Let \[y = f(x)\], such that \[y \in R \cdot \]. Therefore, we can write
\[ \Rightarrow y = \dfrac{1}{x}\]
On cross multiplying we get
\[ \Rightarrow x = \dfrac{1}{y}\]
Here, \[x\] cannot always be a natural number because \[y\] is a real number except zero.
For example, let \[y = 3\] then \[x = \dfrac{1}{3}\], which is not a natural number.
Hence, \[f\] is not onto.

Note: We can also show that \[f:R \cdot \to R \cdot \] defined by \[f(x) = \dfrac{1}{x}\] is onto by a graphical method.
Consider the graph of \[f(x) = \dfrac{1}{x}\] as shown below,

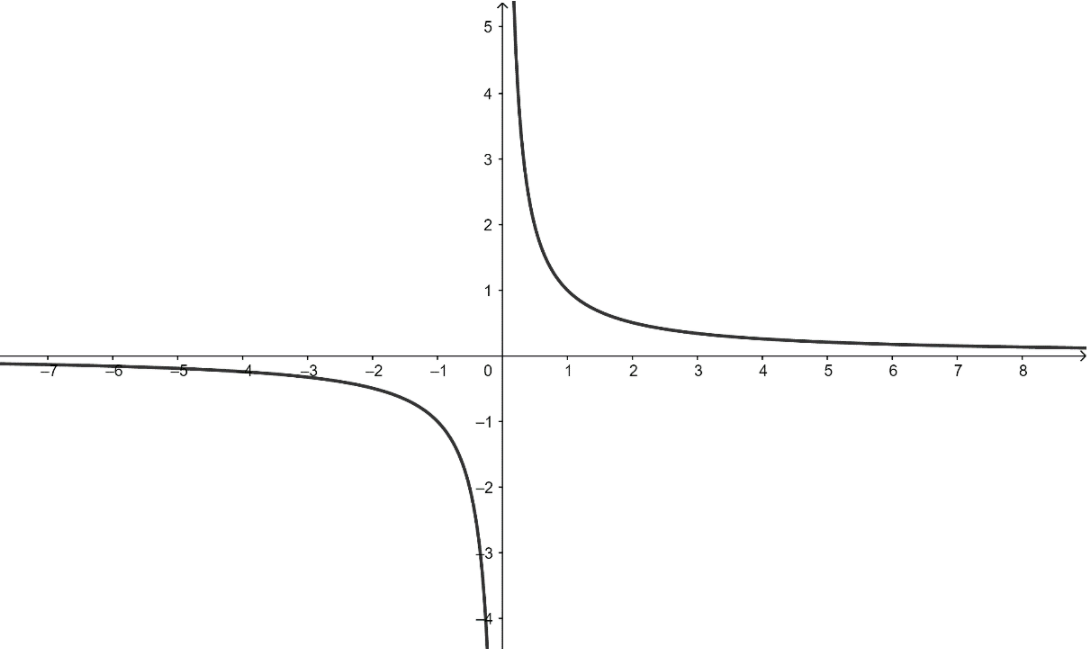
Clearly, we can see that the range of the function \[f:R \cdot \to R \cdot \] defined by \[f(x) = \dfrac{1}{x}\] is \[R - \left\{ 0 \right\}\].
The range of the given function is all real numbers except zero. Hence, the range and codomain of the function are equal.
Therefore, \[f\] is not onto.