
Sides AB, AC and median AD of a triangle ABC are respectively proportional to sides PQ, PR and median PM of another triangle PQR. Show that$\Delta ABC\sim \Delta PQR$.
Answer
504.6k+ views
Hint: First draw a rough sketch of $\Delta ABC$and $\Delta PQR$and then draw construction as to produce AD to E such that AD = DE and PM to F such that PM = MF. Then proof $\Delta ABD\cong \Delta CDE$ and $\Delta PQM\cong \Delta RMF$, using SAS criteria then proof $\Delta ACE\cong \Delta PRF$, using SSS congruence criteria. After that proof $\angle A=\angle P$ using $\angle 1=\angle 2$ and $\angle 3=\angle 4$. Then, in $\Delta ABC$ and $\Delta PQR$, proof $\Delta ABC\sim \Delta PQR$ using SAS similarity criteria.
Complete step-by-step answer:
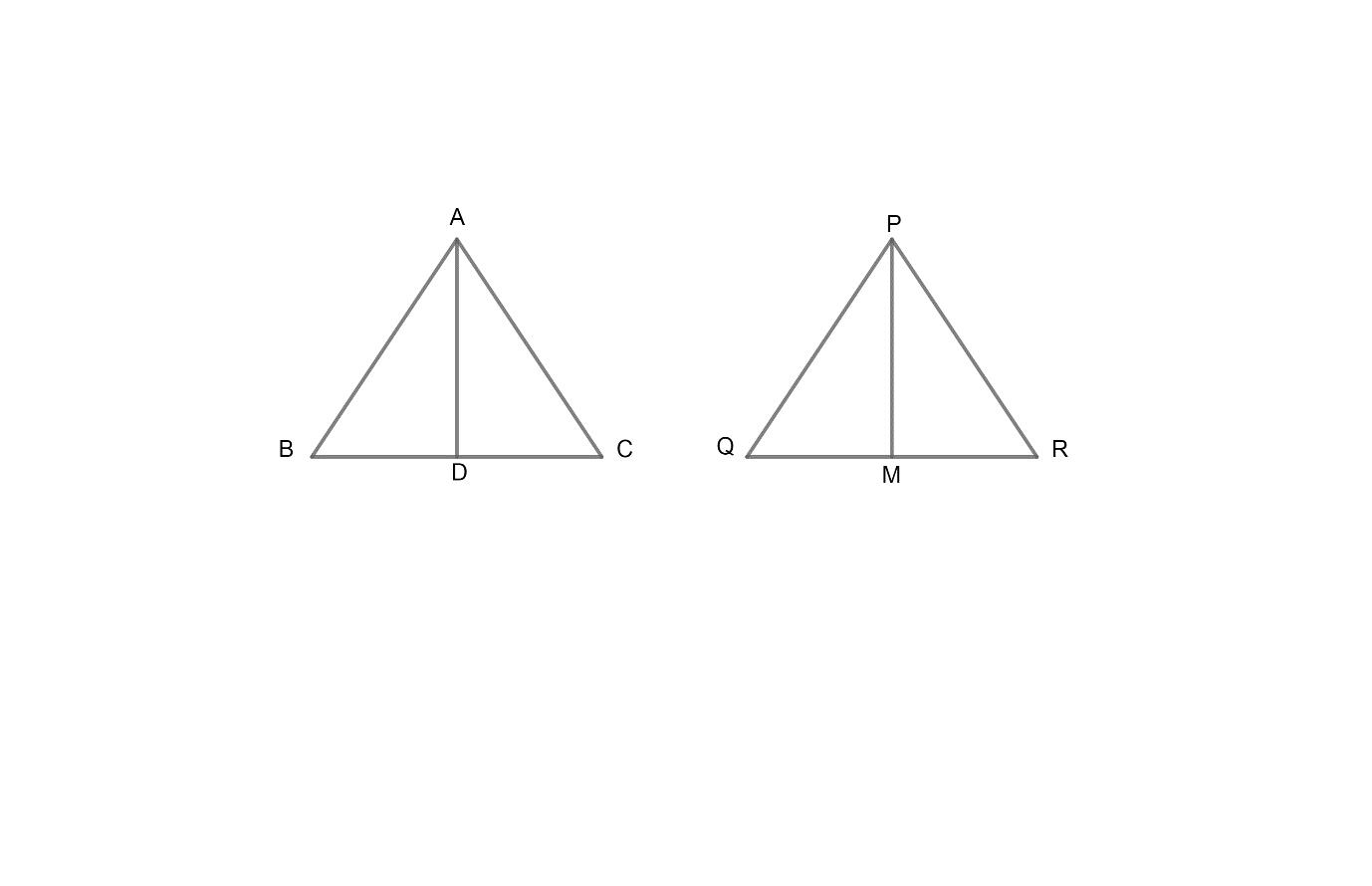
Given, $\Delta ABC$ and $\Delta PQR$in which AD and PM are medians drawn on sides BC and QR respectively.
It is given that , $\dfrac{AB}{PQ}=\dfrac{AC}{PR}=\dfrac{AD}{PM}$
To prove: $\Delta ABC\sim \Delta PQR$.
Construction: Produce AD to E such that AD = DE and PM to F such that PM = MF.

Proof: In $\Delta ABD$and $\Delta CDE$
AD = DE (by construction)
$\angle ADB=\angle CDE$ (Vertically opposite angles) and BD = DC (AD is median)
Therefore, by using SAS congruent condition,
$\Delta ABD\cong \Delta CDE$
$\Rightarrow AB=CE$ (by corresponding parts of congruent triangles i.e. CPCT)
Similarly,
In $\Delta PQM$ and $\Delta RMF$
PM = MF (by construction)
$\angle PMQ=\angle RMF$(Vertically opposite angles)
And QM = MR (PM is a median)
Since, the median divides the opposite side in two equal parts.
Therefore, by using SAS congruence criteria
\[\Delta PQM\cong \Delta RMF\]
\[\Rightarrow PQ=RF\](by CPCT)
It is given that;
$\begin{align}
& \dfrac{AB}{PQ}=\dfrac{AC}{PR}=\dfrac{AD}{PM} \\
& \Rightarrow \dfrac{CE}{RF}=\dfrac{AC}{PR}=\dfrac{2AD}{2PM}\ \ \ \left[ \therefore AB=CE,PQ=RF \right] \\
& \Rightarrow \dfrac{CE}{RF}=\dfrac{AC}{PR}=\dfrac{AE}{PF} \\
\end{align}$
Therefore, by using SSS congruent condition;
$\Delta ACE\cong \Delta PRF$
$\Rightarrow \angle 1=\angle 2.................\left( i \right)$(Demonstrated in figure)
Similarity, $\Rightarrow \angle 3=\angle 4.................\left( ii \right)$(Demonstrated in figure)
Adding equation (i) and (ii), we get,
\[\begin{align}
& \angle 1+\angle 3=\angle 2+\angle 4 \\
& \Rightarrow \angle A=\angle P \\
\end{align}\]
Now, in $\Delta ABC$ and $\Delta PQR$;
$\begin{align}
& \dfrac{AB}{PQ}=\dfrac{AC}{PR} \\
& and\ \angle A=\angle P \\
\end{align}$
Therefore, by using SAS similarity criteria;
$\Delta ABC\sim \Delta PQR$
Note: Students may try in this question to prove $\Delta ABC\sim \Delta PQR$by using SSS similarity criteria. Since, it is given that two sides are already proportional to the two corresponding sides of another triangle, but this approach should not be taken. In this question, it is required to do proper construction and hence to prove $\Delta ABC\sim \Delta PQR$by using SAS similarity criteria.
Complete step-by-step answer:
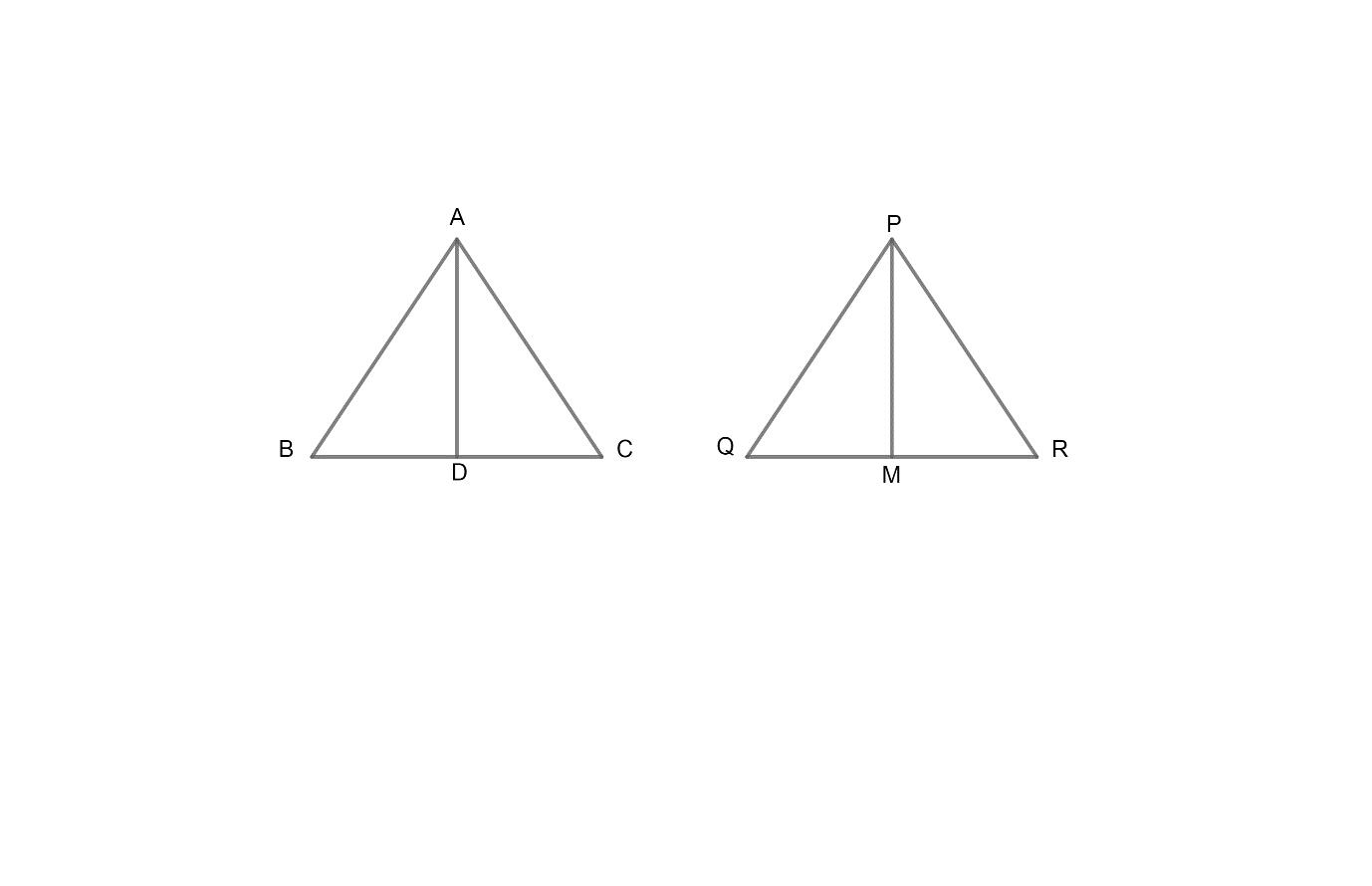
Given, $\Delta ABC$ and $\Delta PQR$in which AD and PM are medians drawn on sides BC and QR respectively.
It is given that , $\dfrac{AB}{PQ}=\dfrac{AC}{PR}=\dfrac{AD}{PM}$
To prove: $\Delta ABC\sim \Delta PQR$.
Construction: Produce AD to E such that AD = DE and PM to F such that PM = MF.

Proof: In $\Delta ABD$and $\Delta CDE$
AD = DE (by construction)
$\angle ADB=\angle CDE$ (Vertically opposite angles) and BD = DC (AD is median)
Therefore, by using SAS congruent condition,
$\Delta ABD\cong \Delta CDE$
$\Rightarrow AB=CE$ (by corresponding parts of congruent triangles i.e. CPCT)
Similarly,
In $\Delta PQM$ and $\Delta RMF$
PM = MF (by construction)
$\angle PMQ=\angle RMF$(Vertically opposite angles)
And QM = MR (PM is a median)
Since, the median divides the opposite side in two equal parts.
Therefore, by using SAS congruence criteria
\[\Delta PQM\cong \Delta RMF\]
\[\Rightarrow PQ=RF\](by CPCT)
It is given that;
$\begin{align}
& \dfrac{AB}{PQ}=\dfrac{AC}{PR}=\dfrac{AD}{PM} \\
& \Rightarrow \dfrac{CE}{RF}=\dfrac{AC}{PR}=\dfrac{2AD}{2PM}\ \ \ \left[ \therefore AB=CE,PQ=RF \right] \\
& \Rightarrow \dfrac{CE}{RF}=\dfrac{AC}{PR}=\dfrac{AE}{PF} \\
\end{align}$
Therefore, by using SSS congruent condition;
$\Delta ACE\cong \Delta PRF$
$\Rightarrow \angle 1=\angle 2.................\left( i \right)$(Demonstrated in figure)
Similarity, $\Rightarrow \angle 3=\angle 4.................\left( ii \right)$(Demonstrated in figure)
Adding equation (i) and (ii), we get,
\[\begin{align}
& \angle 1+\angle 3=\angle 2+\angle 4 \\
& \Rightarrow \angle A=\angle P \\
\end{align}\]
Now, in $\Delta ABC$ and $\Delta PQR$;
$\begin{align}
& \dfrac{AB}{PQ}=\dfrac{AC}{PR} \\
& and\ \angle A=\angle P \\
\end{align}$
Therefore, by using SAS similarity criteria;
$\Delta ABC\sim \Delta PQR$
Note: Students may try in this question to prove $\Delta ABC\sim \Delta PQR$by using SSS similarity criteria. Since, it is given that two sides are already proportional to the two corresponding sides of another triangle, but this approach should not be taken. In this question, it is required to do proper construction and hence to prove $\Delta ABC\sim \Delta PQR$by using SAS similarity criteria.
Recently Updated Pages
Master Class 11 Accountancy: Engaging Questions & Answers for Success

Express the following as a fraction and simplify a class 7 maths CBSE

The length and width of a rectangle are in ratio of class 7 maths CBSE

The ratio of the income to the expenditure of a family class 7 maths CBSE

How do you write 025 million in scientific notatio class 7 maths CBSE

How do you convert 295 meters per second to kilometers class 7 maths CBSE

Trending doubts
The Equation xxx + 2 is Satisfied when x is Equal to Class 10 Maths

Why is there a time difference of about 5 hours between class 10 social science CBSE

Change the following sentences into negative and interrogative class 10 english CBSE

What constitutes the central nervous system How are class 10 biology CBSE

Write a letter to the principal requesting him to grant class 10 english CBSE

Explain the Treaty of Vienna of 1815 class 10 social science CBSE




