Question

What is the significance of binding energy per nucleon of a nucleus?

Answer 1

Hint: Nucleons of a nucleus are nothing but the collection of neutrons and protons in a nucleus. To hold these neutrons and protons in a nucleus together, a certain amount of energy is required. This energy also determines the stability of a nucleus.

Formula used:
\[{{F}_{c}}=m{{\omega }^{2}}{{r}^{'}}\]
\[N=N\cos \theta +N\sin \theta \]
\[W=mg\]

Complete step by step answer:
The collection of subatomic particles or component parts which constitute a nucleus in an atom are called nucleons. These component parts of a nucleus are nothing but neutrons and protons. Nucleons of a nucleus are held together by strong attractive forces among themselves. These strong attractive forces bind the nucleons together to make the nucleus stable.
If one intends to break the nucleus into its component parts, a certain amount of energy has to be applied. This energy, which is required to decompose the nucleus into neutrons and protons is termed as binding energy of a nucleus. On the other hand, to bring neutrons and protons together to form a nucleus, a certain amount of energy has to be liberated. This energy is the same as the energy required to break the nucleus and is called binding energy of the nucleus. Binding energy of a nucleus is given by Einstein’s mass-energy equivalence relation, as given below.
$E=\Delta m{{c}^{2}}$
where $\Delta m$ refers to the mass defect.
Experimentally, it is seen that the mass of a nucleus is less than the sum of masses of its component parts. This difference in mass is referred to as the mass defect. Mass defect disappears when binding energy is liberated or applied to compose or decompose a nucleus, respectively.
Another method to measure the binding energy of neutrons and protons is to determine the binding energy of nucleons. Binding energy of a nucleon is equal to the ratio of binding energy of the nucleus which constitutes the nucleon, to the number of nucleons present in the nucleus. It is given by
${{E}_{b}}=\dfrac{{{E}_{n}}}{A}$
where
${{E}_{b}}$ is the binding energy of a nucleon
${{E}_{n}}$ is the binding energy of the nucleus
$A$ is the total number of nucleons present in the nucleus
Binding energy per nucleon refers to the average energy required by a nucleon to separate a nucleus into individual protons and neutrons. Binding energy per nucleon is a strong attractive force, which binds the nucleons together in a nucleus.
When a heavy nucleus breaks down to its constituent nucleons, it is seen that the binding energy per nucleon is higher than the binding energy of the nucleus itself. This suggests that nucleons are tightly bound after the breakdown. Similarly, when two light nuclei fuse to form a heavy nucleus, it is seen that the binding energy per nucleon of the heavy nucleus is higher than the binding energy per nucleon of lighter nuclei. This suggests that nucleons are tightly bound, after the fusion between two light nuclei to form a heavy nucleus.
If we plot a graph between average binding energy per nucleon and mass number (number of neutrons or protons) of a nucleus, it is seen that atoms having mass number $50-70$ have greater stability than all the other atoms. This is shown in the following graph.

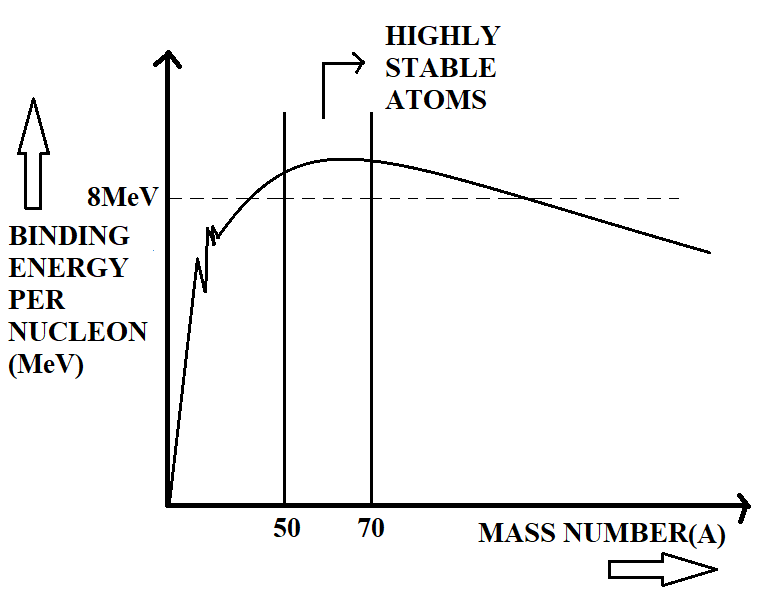
The graph also tells that the average binding energy per nucleon, excluding the lighter nuclei, is about $8MeV$. The lighter nuclei, having low mass numbers have low binding energy per nucleon, and are less stable. They undergo fusion to become a heavy nucleus of more binding energy per nucleon and stability. The heavy nuclei, on the other hand, are also less stable, due to their low binding energy per nucleon. These heavy nuclei undergo fission to become lighter nuclei of high binding energy per nucleon and stability.

Note:
It is important to understand that nuclear forces are short-range forces. The force exerted by a nucleon inside a nucleus is short-ranged. This suggests that binding energy caused by a nucleon will have an effect only on that particular nucleon’s immediate neighbours. Beyond the range of nuclear force, the binding energy of a particular nucleon will have no effect. Therefore, binding energy per nucleon is proportional to the number of neighbouring nucleons, inside a nucleus.