Question

How do you simplify the square root of $243$ ?

Answer 1

Hint: For finding the square root we use prime factorization method. In this method we factorize the numbers into prime factors and then evaluate the given expression.

Complete step-by-step answer:
The objective of the problem is to find the value of $\sqrt {529} $
There are two methods of prime factorization: the division method and the factor tree method.
To find the value of $\sqrt {243} $ we use long division method of prime factorization
Factorization by long division method :
For this first we divide the number by the smallest prime number which is exactly divisible.
Again we divide the obtained quotient by the same or another smallest prime number. Repeat the process until quotient becomes one.
Now consider,
$\begin{gathered}
  3\left| \!{\underline {\,
  {243} \,}} \right. \\
  3\left| \!{\underline {\,
  {81} \,}} \right. \\
  3\left| \!{\underline {\,
  {27} \,}} \right. \\
  3\left| \!{\underline {\,
  9 \,}} \right. \\
  3\left| \!{\underline {\,
  3 \,}} \right. \\
  \,\,\,1 \\
\end{gathered} $
Now we express the given number into a product of prime numbers.
$243 = 3 \times 3 \times 3 \times 3 \times 3 \times 1$
Now take the square roots on both sides we get $\sqrt {243} = \sqrt {3 \times 3 \times 3 \times 3 \times 3 \times 1} $
$\begin{gathered}
  \sqrt {243} = 3 \times 3 \times \sqrt 3 \\
  \,\,\,\,\,\,\,\,\,\,\,\,\, = 9 \times \sqrt 3 \\
\end{gathered} $
The value of \[\sqrt 3 \] is 1.73205
On multiplying the factors we get ,
\[\sqrt {243} = 9 \times 1.73205 = 15.588\]
Hence the square root of 243 is 15.588 approximately.
The given number is not a perfect square.
Factorization by factor tree method:
In this method we draw the prime factors of 243 as factor trees.
In the above steps we already done with factors of 243.
Now draw the factor tree of the given number.

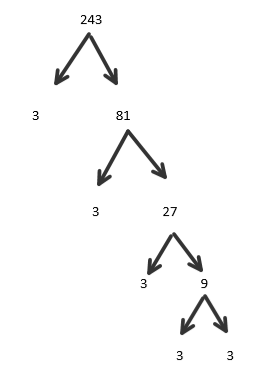
Therefore , the square root of 243 is 15.588 approximately.

Note: The prime factors of a number are the prime numbers that when multiplied it gives the original number. A perfect square is a number where the product of some integer with itself gives the perfect square number. The perfect square numbers are non negative.