Question

How do you sketch the angle ${{195}^{\circ }}$ and find its reference angle?

Answer 1

Hint: We can sketch only acute angles, that is the angles which are less than ${{90}^{\circ }}$ with the common reference angle of ${{0}^{\circ }}$. But for the angles greater than ${{90}^{\circ }}$, we need to change the reference angle. The reference angle is always an integral multiple of ${{90}^{\circ }}$. Therefore, we will write the given angle of ${{195}^{\circ }}$ as ${{195}^{\circ }}={{180}^{\circ }}+{{15}^{\circ }}$ so that the reference angle will be equal to ${{180}^{\circ }}$ with the respect of which the given angle can be sketched at an angle of \[{{15}^{\circ }}\] to it.

Complete step by step solution:
Let us write the value of the angle given in the above question as
$ A={{195}^{\circ }}$
The given angle is greater than ${{90}^{\circ }}$. Therefore, it is not simple to sketch. For this, we first need to divide it by ${{90}^{\circ }}$ to get
$\begin{align}
  & \Rightarrow A={{90}^{\circ }}\times 2+{{15}^{\circ }} \\
 & \Rightarrow A={{180}^{\circ }}+{{15}^{\circ }} \\
\end{align}$
So we have obtained the angle of ${{15}^{\circ }}$ which is an acute angle, and therefore it is simple to sketch. But it cannot be sketched using ${{0}^{\circ }}$ as the reference. From the above equation, the reference angle is of ${{180}^{\circ }}$. So it will be sketched as below.

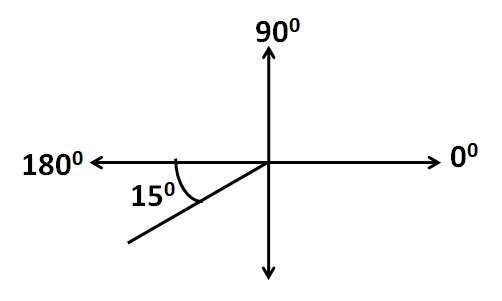
Hence, the given angle of ${{195}^{\circ }}$ is sketched with the reference angle of ${{180}^{\circ }}$.

Note: Do not be confused by the angle ${{15}^{\circ }}$ as shown in the sketch drawn in the above solution. We must notice the reference angle with respect to which it has been drawn. Since it has been drawn with ${{180}^{\circ }}$ as the reference angle, ${{180}^{\circ }}$ has to be added to ${{15}^{\circ }}$ so that the total angle shown above is of ${{195}^{\circ }}$ and not of ${{15}^{\circ }}$.