Question

Solve the following.
1. It is given that $ \Delta ABC \sim \Delta PQR $ with $ \dfrac{{BC}}{{QR}} = \dfrac{1}{3} $ then, $ \dfrac{{Ar\left( {\Delta PRQ} \right)}}{{Ar\left( {\Delta BCA} \right)}} $ is equal to:
 A. 9
B. 3
C. $ \dfrac{1}{3} $
D. $ \dfrac{1}{9} $

2. Ratio in which the line $ 3x + 4y = 7 $ divides the line segment joining the points $ \left( {1,2} \right) $ and $ \left( { - 2,1} \right) $ is:

Answer 1

Hint: If two triangles are similar, then the ratio of the areas of both the triangles is equal to the ratio of the squares of their corresponding sides. Here the ratio of the sides of the triangles is given. Using this, we are finding the ratio of their areas.
2. Let the point at which the line $ 3x + 4y = 7 $ touches the line segment joining the points $ \left( {1,2} \right) $ and $ \left( { - 2,1} \right) $ is $ P\left( {x,y} \right) $ and divides the line segment in the ratio $ m:n $ , then the coordinates of P can be found by $ x = \dfrac{{m{x_2} + n{x_1}}}{{m + n}},y = \dfrac{{m{y_2} + n{y_1}}}{{m + n}} $ , where $ \left( {{x_1},{y_1}} \right),\left( {{x_2},{y_2}} \right) $ are the given points. The point $ P\left( {x,y} \right) $ lies on the line $ 3x + 4y = 7 $ . So substitute its coordinates in the place of x and y of $ 3x + 4y = 7 $ to find the ratio of m and n.

Complete step-by-step answer:
1. We are given that the triangle ABC is similar to the triangle PQR.

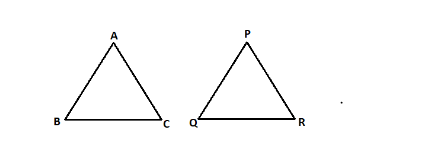
And the ratio of sides $ \dfrac{{BC}}{{QR}} = \dfrac{1}{3} $ .
Then the ratio of areas of triangles ABC and PQR will be $ \dfrac{{Ar\left( {\Delta PQR} \right)}}{{Ar\left( {\Delta ABC} \right)}} = \dfrac{{Ar\left( {\Delta PRQ} \right)}}{{Ar\left( {\Delta BCA} \right)}} = {\left( {\dfrac{{QR}}{{BC}}} \right)^2} $
We already know that $ \dfrac{{BC}}{{QR}} = \dfrac{1}{3} $ , this gives $ \dfrac{{QR}}{{BC}} = \dfrac{3}{1} $
Therefore,
 $ \dfrac{{Ar\left( {\Delta PRQ} \right)}}{{Ar\left( {\Delta BCA} \right)}} = {\left( {\dfrac{3}{1}} \right)^2} = \dfrac{9}{1} = 9 $
So, the correct answer is “ OPTION A”.

2. We are given that line $ 3x + 4y = 7 $ divides the line segment joining the points $ \left( {1,2} \right) $ and $ \left( { - 2,1} \right) $ . Let the line divide the line segment at point $ P\left( {x,y} \right) $ in a ratio $ m:n $ .

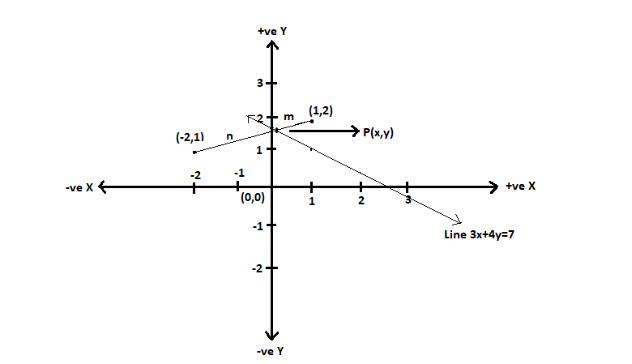
Then the coordinates of point $ P\left( {x,y} \right) $ will be $ \left( {\dfrac{{m{x_2} + n{x_1}}}{{m + n}},\dfrac{{m{y_2} + n{y_1}}}{{m + n}}} \right) $ , where $ \left( {{x_1},{y_1}} \right),\left( {{x_2},{y_2}} \right) $ are the given points and $ \left( {{x_1},{y_1}} \right) = \left( {1,2} \right),\left( {{x_2},{y_2}} \right) = \left( { - 2,1} \right) $ , and as we can see the point $ P\left( {x,y} \right) $ lies on the line $ 3x + 4y = 7 $
So we are substituting $ \left( {\dfrac{{m{x_2} + n{x_1}}}{{m + n}},\dfrac{{m{y_2} + n{y_1}}}{{m + n}}} \right) $ in the place of x and y of $ 3x + 4y = 7 $
 $ 3\left( {\dfrac{{m{x_2} + n{x_1}}}{{m + n}}} \right) + 4\left( {\dfrac{{m{y_2} + n{y_1}}}{{m + n}}} \right) = 7 $
 $ \Rightarrow 3m{x_2} + 3n{x_1} + 4m{y_2} + 4n{y_1} = 7\left( {m + n} \right) $
 $ {x_1} = 1,{y_1} = 2,{x_2} = - 2,{y_2} = 1 $
 $ \Rightarrow 3m\left( { - 2} \right) + 3n\left( 1 \right) + 4m\left( 1 \right) + 4n\left( 2 \right) = 7m + 7n $
 $ \Rightarrow - 6m + 3n + 4m + 8n = 7m + 7n $
 $ \Rightarrow - 2m + 11n = 7m + 7n $
 $ \Rightarrow 11n - 7n = 7m + 2m $
 $ \Rightarrow 4n = 9m $
 $ \Rightarrow \dfrac{4}{9} = \dfrac{m}{n} $
 $ \Rightarrow m:n = 4:9 $
Therefore, the line $ 3x + 4y = 7 $ divides the line segment joining the points $ \left( {1,2} \right) $ and $ \left( { - 2,1} \right) $ in the ratio 4:9.
So, the correct answer is “ 4:9”.

Note: Do not confuse similar triangles with congruent triangles, because congruent triangles have similar three sides and angles which mean similar areas, whereas the areas may or may not be the same in similar triangles. Congruent triangles are always similar whereas similar triangles may not be congruent always. A line can divide another line both internally and externally. When a line divides a line segment AB internally it produces a division point between A and B whereas when externally it produces a division point outside AB.