
How do you solve $y = 4x - 3$ and $y = 1$ by graphing and classifying the system?
Answer
400.5k+ views
Hint: In the question, we are provided with two equations that represent straight lines on the Cartesian plane. We plot the graphs of the straight lines by finding the coordinates of some points lying on the line. We substitute the value of $x$ and we determine the value of $y$ and then we mark the points in the graph and we join the points.
Complete step by step answer:
So, we have the equations: $y = 4x - 3$ and $y = 1$.
So, we have to graph the straight lines on the Cartesian plane.
First, we find the coordinates of points lying on the line $y = 4x - 3$.
We find the values of y by using the graph equation $y = 4x - 3$. Let us substitute the value of x as $0$, $1$, and $\dfrac{1}{2}$.
Now we consider the value of x as $0$, the value of y is
\[ \Rightarrow y = 4\left( 0 \right) - 3\]
\[ \Rightarrow y = - 3\]
Now we consider the value of x as $1$, the value of y is
\[ \Rightarrow y = 4\left( 1 \right) - 3\]
\[ \Rightarrow y = 4 - 3\]
\[ \Rightarrow y = 1\]
Now we consider the value of x as $\dfrac{1}{2}$, the value of y is
\[ \Rightarrow y = 4\left( {\dfrac{1}{2}} \right) - 3\]
\[ \Rightarrow y = 2 - 3\]
\[ \Rightarrow y = - 1\]
Now we draw a table for these values we have
Similarly, we have to find the coordinates of points lying on the line $y = 1$.
Let us substitute the value of x as $0$, $1$, and $2$.
Now we consider the value of x as $0$, the value of y is
\[ \Rightarrow y = 1\]
Now we consider the value of x as $1$, the value of y is
\[ \Rightarrow y = 1\]
Now we consider the value of x as $2$, the value of y is
\[ \Rightarrow y = 1\]
Now we draw a table for these values we have
Now, we plot the graphs for both the equations. So, we get,
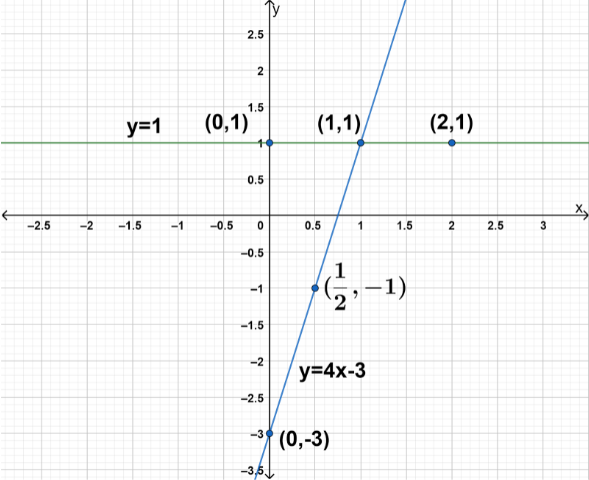
Now, we can see that the straight lines represented by the two equations intersect each other at a single unique point. So, the system of equations is consistent and possesses a unique solution.
Note: The graph plotted is of two dimensional. The graph is plotted in x-axis versus y axis. By the equation of a graph, we can plot the graph by assuming the value of $x$ and finding the corresponding values of $y$. Consistent system of equations is the system of equations that possess a solution, either a unique solution or infinitely many solutions.
Complete step by step answer:
So, we have the equations: $y = 4x - 3$ and $y = 1$.
So, we have to graph the straight lines on the Cartesian plane.
First, we find the coordinates of points lying on the line $y = 4x - 3$.
We find the values of y by using the graph equation $y = 4x - 3$. Let us substitute the value of x as $0$, $1$, and $\dfrac{1}{2}$.
Now we consider the value of x as $0$, the value of y is
\[ \Rightarrow y = 4\left( 0 \right) - 3\]
\[ \Rightarrow y = - 3\]
Now we consider the value of x as $1$, the value of y is
\[ \Rightarrow y = 4\left( 1 \right) - 3\]
\[ \Rightarrow y = 4 - 3\]
\[ \Rightarrow y = 1\]
Now we consider the value of x as $\dfrac{1}{2}$, the value of y is
\[ \Rightarrow y = 4\left( {\dfrac{1}{2}} \right) - 3\]
\[ \Rightarrow y = 2 - 3\]
\[ \Rightarrow y = - 1\]
Now we draw a table for these values we have
| x | $0$ | $1$ | $\dfrac{1}{2}$ |
| y | $ - 3$ | $1$ | $ - 1$ |
Similarly, we have to find the coordinates of points lying on the line $y = 1$.
Let us substitute the value of x as $0$, $1$, and $2$.
Now we consider the value of x as $0$, the value of y is
\[ \Rightarrow y = 1\]
Now we consider the value of x as $1$, the value of y is
\[ \Rightarrow y = 1\]
Now we consider the value of x as $2$, the value of y is
\[ \Rightarrow y = 1\]
Now we draw a table for these values we have
| x | $0$ | $1$ | $2$ |
| y | $1$ | $1$ | $1$ |
Now, we plot the graphs for both the equations. So, we get,

Now, we can see that the straight lines represented by the two equations intersect each other at a single unique point. So, the system of equations is consistent and possesses a unique solution.
Note: The graph plotted is of two dimensional. The graph is plotted in x-axis versus y axis. By the equation of a graph, we can plot the graph by assuming the value of $x$ and finding the corresponding values of $y$. Consistent system of equations is the system of equations that possess a solution, either a unique solution or infinitely many solutions.
Recently Updated Pages
Express the following as a fraction and simplify a class 7 maths CBSE

The length and width of a rectangle are in ratio of class 7 maths CBSE

The ratio of the income to the expenditure of a family class 7 maths CBSE

How do you write 025 million in scientific notatio class 7 maths CBSE

How do you convert 295 meters per second to kilometers class 7 maths CBSE

Write the following in Roman numerals 25819 class 7 maths CBSE

Trending doubts
When people say No pun intended what does that mea class 8 english CBSE

In Indian rupees 1 trillion is equal to how many c class 8 maths CBSE

How many ounces are in 500 mL class 8 maths CBSE

Which king started the organization of the Kumbh fair class 8 social science CBSE

What is BLO What is the full form of BLO class 8 social science CBSE

Advantages and disadvantages of science




