
What is the spring constant in parallel connection and series connection?
Answer
423.9k+ views
Hint: Two massless springs that follow Hooke's Law are said to be connected in parallel when they are connected by a thin, vertical rod, as shown in the diagram below. The formula for capacitors connected in parallel in an electrical circuit can be used to find the value of k.
Complete answer:
For parallel:
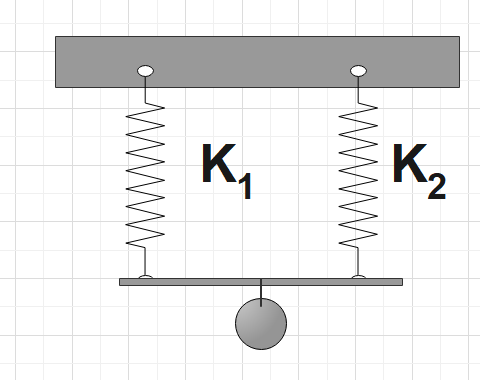
Two massless springs that follow Hooke's Law are said to be connected in parallel when they are connected by a thin, vertical rod.
A single Hookean spring of spring constant
For Series
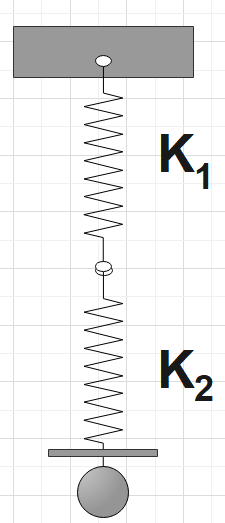
Here the equivalent spring constant would be,
When the same springs are connected in series, as shown in the diagram below, this is referred to as a series connection. On spring 2, a constant force F is applied. As a result, the springs are elongated, and the total extension of the combination equals the sum of each spring's elongation. Alternatively, the springs could be compressed by reversing the force direction.
A single spring of spring constant k is equivalent to this system of two springs in series. The formula for capacitors connected in series in an electrical circuit can be used to calculate the value of k.
Note: When two or more springs are connected end-to-end or point-to-point in mechanics, they are said to be in series, and when they are connected side-by-side, they are said to be in parallel; in both cases, they act as a single spring.
Complete answer:
For parallel:

Two massless springs that follow Hooke's Law are said to be connected in parallel when they are connected by a thin, vertical rod.
A single Hookean spring of spring constant
For Series

Here the equivalent spring constant would be,
When the same springs are connected in series, as shown in the diagram below, this is referred to as a series connection. On spring 2, a constant force F is applied. As a result, the springs are elongated, and the total extension of the combination equals the sum of each spring's elongation. Alternatively, the springs could be compressed by reversing the force direction.
A single spring of spring constant k is equivalent to this system of two springs in series. The formula for capacitors connected in series in an electrical circuit can be used to calculate the value of k.
Note: When two or more springs are connected end-to-end or point-to-point in mechanics, they are said to be in series, and when they are connected side-by-side, they are said to be in parallel; in both cases, they act as a single spring.
Recently Updated Pages
Express the following as a fraction and simplify a class 7 maths CBSE

The length and width of a rectangle are in ratio of class 7 maths CBSE

The ratio of the income to the expenditure of a family class 7 maths CBSE

How do you write 025 million in scientific notatio class 7 maths CBSE

How do you convert 295 meters per second to kilometers class 7 maths CBSE

Write the following in Roman numerals 25819 class 7 maths CBSE

Trending doubts
State and prove Bernoullis theorem class 11 physics CBSE

What are Quantum numbers Explain the quantum number class 11 chemistry CBSE

Write the differences between monocot plants and dicot class 11 biology CBSE

Who built the Grand Trunk Road AChandragupta Maurya class 11 social science CBSE

1 ton equals to A 100 kg B 1000 kg C 10 kg D 10000 class 11 physics CBSE

State the laws of reflection of light




