Question

How many squares are there in a chess board?
A. 1296
B.204
C. 120
D. 130

Answer 1

Hint: This is a trick question since one might get confused and at once calculate the total number of squares in a eight rows and eight columns chessboard by (number of rows $ \times $ number of columns= $ 8 \times 8 = 64 $ ) but these squares are only the similar squares of let say unit length.

Complete step-by-step answer:
Therefore to calculate overall squares we need to include the squares made by four unit length squares arranged together and similarly the larger squares as well.

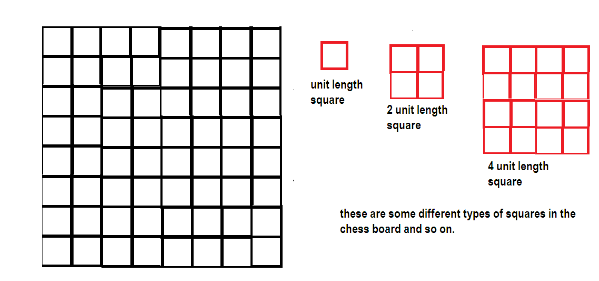
Therefore we can observe 16 squares of two unit length although they are not the only squares with unit length 2 in this chess board there are more, similarly for three unit length and so on we can calculate the number of squares in this chess board the different sized squares are:
 $
  8 \times 8 \\
  7 \times 7 \\
  6 \times 6 \\
  ... \\
  2 \times 2 \\
  1 \times 1 \;
 $
Therefore it can be enlisted as
 $ {1^2} + {2^2} + {3^2} + {4^2} + {5^2} + {6^2} + {7^2} + {8^2} $ =1+4+9+25+36+49+64
We can understand it better by writing the above as sum of squares of first eight numbers which can be calculated as
 $\Rightarrow \sum {n^2} = \dfrac{{n(n + 1)(2n + 1)}}{6} $
Where n is the value for the first natural numbers and the formula gives the value for the sum of squares of first n natural numbers and here the value of n is 8. Therefore substituting the values we get,
 $
\Rightarrow \sum {8^2} = \dfrac{{8(8 + 1)(2 \times 8 + 1)}}{6} = \dfrac{{8(9)(16 + 1)}}{6} = \dfrac{{72 \times 17}}{6} = 12 \times 17 \\
\Rightarrow \sum {8^2} = 12 \times 17 = 204 \;
 $
 Hence there are 204 squares in total in a eight rows and eight columns chess board.
So, the correct answer is “204”.

Note: We must carefully note that the trend of the numbers in the above case was adding the squares of the first eight natural numbers which is the above formula was applicable. Also note that the biggest square is the one with eight squares in the row and column.