
State Ampere’s circuital law.
Answer
435.3k+ views
5 likes
Hint: In this question consider a straight current carrying wire since current is simply flow of electrons and this flow of electrons give rise to a magnetic field thus magnetic fields and also consider an imaginary loop around this conductor as shown also known as imperial loop of radius r, so write the magnetic field at any point on this loop. This will help approaching the problem.
Step By Step Answer:
Ampere’s Circuital law:
It is the relationship between the current and the magnetic field created by the current.
So according to this law the integral of magnetic field density (B) along an imaginary path is equal to the product of the permeability of the free space and the current enclosed by the path.
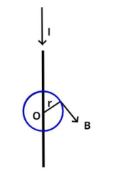
Let us consider an electrical conductor which carries current I in the downward direction as shown in the figure, we also consider an imaginary loop around this conductor as shown also known as amperian loop, so due to this the magnetic field at any point on this loop is given as,
Where,
This law is the basis of the Biot – savart law
Biot – savart law –
The Biot-Savart Law is an equation that describes the magnetic field created by a current-carrying wire and allows you to calculate its strength at various points.
Biot Savart Law
Note: The same role ampere’s circuital law plays in magnetic physics the same is played by Gauss Law in electrostatic physics. The common thing about Gauss law and ampere circuital law is that both are applied to the systems in which the current flowing has symmetrical distribution.
Step By Step Answer:
Ampere’s Circuital law:
It is the relationship between the current and the magnetic field created by the current.
So according to this law the integral of magnetic field density (B) along an imaginary path is equal to the product of the permeability of the free space and the current enclosed by the path.

Let us consider an electrical conductor which carries current I in the downward direction as shown in the figure, we also consider an imaginary loop around this conductor as shown also known as amperian loop, so due to this the magnetic field at any point on this loop is given as,
Where,
This law is the basis of the Biot – savart law
Biot – savart law –
The Biot-Savart Law is an equation that describes the magnetic field created by a current-carrying wire and allows you to calculate its strength at various points.
Biot Savart Law
Note: The same role ampere’s circuital law plays in magnetic physics the same is played by Gauss Law in electrostatic physics. The common thing about Gauss law and ampere circuital law is that both are applied to the systems in which the current flowing has symmetrical distribution.
Recently Updated Pages
Master Class 4 Maths: Engaging Questions & Answers for Success

Master Class 4 English: Engaging Questions & Answers for Success

Master Class 4 Science: Engaging Questions & Answers for Success

Class 4 Question and Answer - Your Ultimate Solutions Guide

Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Trending doubts
Give 10 examples of unisexual and bisexual flowers

Draw a labelled sketch of the human eye class 12 physics CBSE

a Tabulate the differences in the characteristics of class 12 chemistry CBSE

Differentiate between homogeneous and heterogeneous class 12 chemistry CBSE

Why is the cell called the structural and functional class 12 biology CBSE

Differentiate between insitu conservation and exsitu class 12 biology CBSE




