
State and explain Ampere’s circuital law.
Answer
494.7k+ views
Hint: Ampere's circuital law states that the closed line integral of magnetic field around a current carrying conductor is equal to absolute permeability times the total current threading the conductor. We can formulate it mathematically and understand the concept well.
Complete step-by-step answer:
Amperes circulate law mathematically state that the line integral of magnetic field of induction B around any closed path in free space is equal to absolute permeability of free space
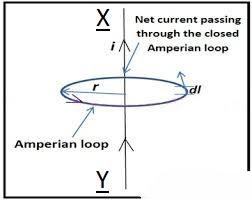
Mathematically, we can that the law as,
B is magnetic induction
I is the total current flowing through the wire
Dl is length element of path
where,
Note: Ampere's law gives us another method to calculate the magnetic field due to a given current distribution in a given fashion. Ampere's law can be derived from the Biot-Savart law and Biot-Savart law can also be derived from Ampere's law. Ampere's law is more useful under certain conditions where current distribution is symmetrical. We can calculate the magnetic field in a solenoid using this law.
Complete step-by-step answer:
Amperes circulate law mathematically state that the line integral of magnetic field of induction B around any closed path in free space is equal to absolute permeability of free space

Mathematically, we can that the law as,
B is magnetic induction
I is the total current flowing through the wire
Dl is length element of path
where,
Note: Ampere's law gives us another method to calculate the magnetic field due to a given current distribution in a given fashion. Ampere's law can be derived from the Biot-Savart law and Biot-Savart law can also be derived from Ampere's law. Ampere's law is more useful under certain conditions where current distribution is symmetrical. We can calculate the magnetic field in a solenoid using this law.
Recently Updated Pages
Master Class 12 Economics: Engaging Questions & Answers for Success

Master Class 12 Maths: Engaging Questions & Answers for Success

Master Class 12 Biology: Engaging Questions & Answers for Success

Master Class 12 Physics: Engaging Questions & Answers for Success

Master Class 4 Maths: Engaging Questions & Answers for Success

Master Class 4 English: Engaging Questions & Answers for Success

Trending doubts
Give 10 examples of unisexual and bisexual flowers

Draw a labelled sketch of the human eye class 12 physics CBSE

a Tabulate the differences in the characteristics of class 12 chemistry CBSE

Differentiate between homogeneous and heterogeneous class 12 chemistry CBSE

Why is the cell called the structural and functional class 12 biology CBSE

Differentiate between insitu conservation and exsitu class 12 biology CBSE




