Question

State and explain Biot- savart’s law.

Answer 1

Hint: The Biot–Savart’s law is an equation describing the magnetic field generated by a constant electric current. It relates the magnetic field to the magnitude, direction, length, and electric current.

Complete step by step answer:
Biot-savart’s law is used to determine the strength of a magnetic field at any point due to a current-carrying conductor.
Consider a very small element AB of the length $dl$ of a conductor carrying current I. The strength of magnetic field $dB$ due to this small current element at a point $P$, distance $r$ from the element is found to depend upon quantities;

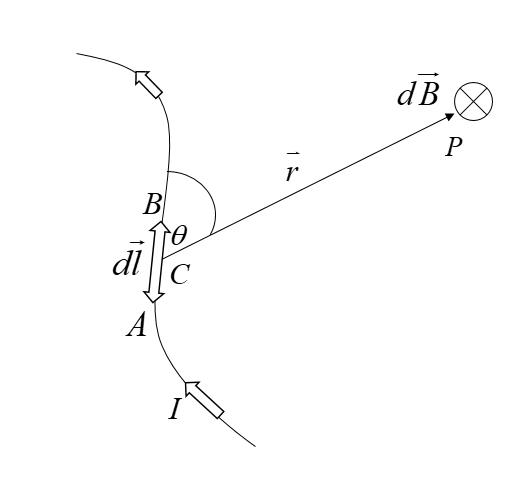
i)${\rm{db}} \propto {\rm{ dl}}$
ii) ${\rm{dB}} \propto {\rm{I}}$
iii) ${\rm{dB}} \propto {\rm{sin}}\theta $, where$\theta $ is the angle between ${\rm{d\vec l}}$ and ${\rm{\vec r}}$ vector
iv) ${\rm{dB}} \propto \dfrac{1}{{{{\rm{r}}^2}}}$
On combining (i) to (iv), we get ${\rm{dB}} \propto \dfrac{{{\rm{Idlsin}}\theta }}{{{r^2}}}$
i.e. ${\rm{dB = }}k\dfrac{{{\rm{Idlsin}}\theta }}{{{r^2}}}$
Where k is the constant of proportionality.
In SI units, ${\rm{k}} = \dfrac{{{\mu _0}}}{{4\pi }}$ where ${\mu _0}$ is called absolute permeability.

Additional information:
Some of the Biot-savart’s law applications are:
- We can use it to calculate magnetic responses even at the atomic or molecular level.
- It is also used in aerodynamic theory to calculate the velocity induced by vortex lines.

Note:
Biot-savart’s law is similar to coulomb’s law in electrostatics. This law is applicable for very small conductors too which vary current. It is also applicable for symmetrical current distribution. Biot–Savart law has evenness with both Ampere's circuital law and Gauss's theorem.