Question

State and prove BPT.

Answer 1

Hint: First, we draw a triangle ABC and draw straight line DE passes through two sides of the triangle and parallel to the third side. Now, we have to prove that the ratio of AD and DB is equal as it is divided by point D. By using this methodology, we can easily solve our problem.

Complete step-by-step answer:
Statement: If a line passes through two sides of a triangle, then it is parallel to the third side that divides the other two sides in the same ratio.
First, we draw a triangle ABC and draw straight line DE passes two sides of the triangle and parallel to the third side. This can be shown as:

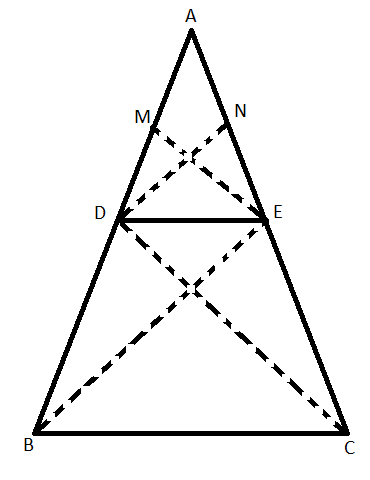
In $\Delta ADE$, considering base to be AD and height to be ME.
Area of triangle ADE$=\dfrac{1}{2}\times AD\times ME...(1)$
Again, taking triangle ADE, but this time base is AE and height is ND.
In $\Delta ADE$,
Area of triangle ADE$=\dfrac{1}{2}\times AE \times ND...(2)$
In $\Delta BDE$, where base is DB and height is ME:
Area of triangle BDE$=\dfrac{1}{2}\times DB\times ME...(3)$
In $\Delta DEC,$ where base is EC and height is ND
Area of triangle DEC$=\dfrac{1}{2}\times EC\times ND...(4)$
Now, we divide Equation (1) and (3) to obtain equation (5)
$\begin{align}
  & \dfrac{area(\Delta ADE)}{area(\Delta BDE)}=\dfrac{\dfrac{1}{2}\times AD\times ME}{\dfrac{1}{2}\times DB\times ME} \\
 & \dfrac{area(\Delta ADE)}{area(\Delta BDE)}=\dfrac{AD}{DB}...(5) \\
\end{align}$
Now, divide equation (2) and equation (4) to obtain equation (6)
$\begin{align}
  & \dfrac{area(\Delta ADE)}{area(\Delta DEC)}=\dfrac{\dfrac{1}{2}\times AE\times ND}{\dfrac{1}{2}\times EC\times ND} \\
 & \dfrac{area(\Delta ADE)}{area(\Delta BDE)}=\dfrac{AE}{EC}...(6) \\
\end{align}$
By using the theorem,
$\begin{align}
  & area\left( \Delta ADE \right)=area\left( \Delta DEC \right) \\
 & \dfrac{area(\Delta ADE)}{area(\Delta BDC)}=\dfrac{area(\Delta ADE)}{area(\Delta DEC)}=\dfrac{AD}{BD} \\
 & \dfrac{area(\Delta ADE)}{area(\Delta DEC)}=\dfrac{AD}{BD}...(7) \\
\end{align}$
By the equation (6) and equation (7), we can rewrite it as
\[\begin{align}
  & \dfrac{AE}{EC}=\dfrac{AD}{BD} \\
 & \therefore \dfrac{AD}{BD}=\dfrac{AE}{EC} \\
\end{align}\]
Hence, we proved the existence of BPT.

Note: The key concept involved in solving this problem is the knowledge of the area of the triangle by considering different bases and height corresponding to that base. By using this consideration, we manipulate the obtained equations to prove the existence of BPT.