Question

State and prove Brewster’s law.

Answer 1

Hint: Brewster’s law states that an unpolarized light ray gets polarized maximum when it falls at a certain angle of incidence, called the Brewster’s angle onto an interface of another medium. The reflected and refracted rays are perpendicular to each other. The reflected ray is completely polarized.

Formula used:
When light travels from a medium of optical density ${{n}_{1}}$ to a medium of optical density ${{n}_{2}}$, the angle of incidence ${{\theta }_{i}}$ is related to the angle of reflection ${{\theta }_{r}}$ by

${{n}_{1}}\sin {{\theta }_{i}}={{n}_{2}}\sin {{\theta }_{r}}$ $\left( \text{Snell }\!\!'\!\!\text{ s Law} \right)$

According to the laws of reflection, when light is reflected by a surface, the angle of incidence ${{\theta }_{i}}$ is equal to the angle of reflection ${{\theta }_{refl}}$. That is,
${{\theta }_{i}}={{\theta }_{refl}}$

Complete step by step answer:
Brewster’s law is a statement that says that when unpolarized light falls on an interface, the reflected light is completely polarized if the angle of incidence is a specific angle called the Brewster’s angle. In this case the angle made by the refracted ray and the reflected ray is ${{90}^{0}}$.

Let us draw a diagram to understand this better.

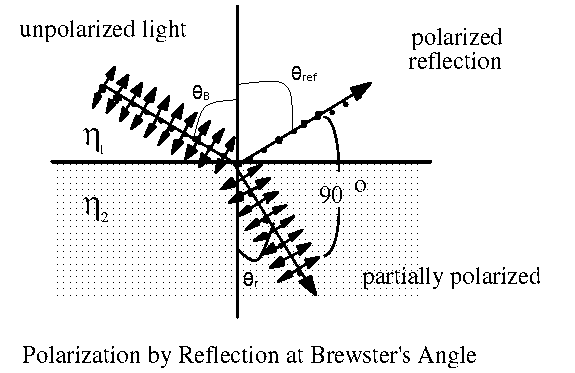
We will draw up a relation between the properties of the two media and the Brewster’s angle.

As shown in the figure, an unpolarized light ray falls on an interface between two media of respective optical densities ${{\eta }_{1}}$ and ${{\eta }_{2}}$ at the Brewster’s angle of incidence ${{\theta }_{B}}$. The angle of reflection is ${{\theta }_{ref}}$ and the angle of refraction is ${{\theta }_{r}}$. The reflected and refracted ray are perpendicular to each other and the reflected ray is completely polarized in one direction.

Now, when light travels from a medium of optical density ${{n}_{1}}$ to a medium of optical density ${{n}_{2}}$, the angle of incidence ${{\theta }_{i}}$ is related to the angle of reflection ${{\theta }_{r}}$ by

${{n}_{1}}\sin {{\theta }_{i}}={{n}_{2}}\sin {{\theta }_{r}}$ $\left( \text{Snell }\!\!'\!\!\text{ s Law} \right)$ ---(1)

According to the laws of reflection, when light is reflected by a surface, the angle of incidence ${{\theta }_{i}}$ is equal to the angle of reflection ${{\theta }_{refl}}$. That is,
${{\theta }_{i}}={{\theta }_{refl}}$ --(2)

Hence, using (1), we get,

${{\eta }_{1}}\sin {{\theta }_{B}}={{\eta }_{2}}\sin {{\theta }_{r}}$
$\therefore \sin {{\theta }_{r}}=\dfrac{{{\eta }_{1}}}{{{\eta }_{2}}}\sin {{\theta }_{B}}$ --(3)


From the figure’s geometry, we get,

${{\theta }_{ref}}+{{90}^{0}}+{{\theta }_{r}}={{180}^{0}}$ (Since, the angle of a straight line is ${{180}^{0}}$)
$\therefore {{\theta }_{ref}}+{{\theta }_{r}}={{180}^{0}}-{{90}^{0}}={{90}^{0}}$
$\therefore {{\theta }_{r}}={{90}^{0}}-{{\theta }_{ref}}$ ---(4)

Now, according to (2),

${{\theta }_{B}}={{\theta }_{ref}}$
$\therefore {{\theta }_{r}}={{90}^{0}}-{{\theta }_{B}}$ [Using (4)] --(5)

Using (3) and (5), we get,

$\sin \left( {{90}^{0}}-{{\theta }_{B}} \right)=\dfrac{{{\eta }_{1}}}{{{\eta }_{2}}}\sin {{\theta }_{B}}$
$\therefore \cos {{\theta }_{B}}=\dfrac{{{\eta }_{1}}}{{{\eta }_{2}}}\sin {{\theta }_{B}}$ $\left( \because \sin \left( {{90}^{0}}-\theta \right)=\cos \theta \right)$
$\therefore \dfrac{{{\eta }_{2}}}{{{\eta }_{1}}}=\dfrac{\sin {{\theta }_{B}}}{\cos {{\theta }_{B}}}=\tan {{\theta }_{B}}$ $\left( \because \dfrac{\sin \theta }{\cos \theta }=\tan \theta \right)$
$\therefore {{\eta }_{21}}=\tan {{\theta }_{B}}$

where $\left( {{\eta }_{21}}=\dfrac{{{\eta }_{2}}}{{{\eta }_{1}}} \right)$ is the refractive index of medium 2 with respect to medium 1.

$\therefore {{\theta }_{B}}={{\tan }^{-1}}\left( {{\eta }_{21}} \right)$

Therefore, we have found a relation for the Brewster’s angle of incidence and the optical properties of the two media.

Note: Students must be familiar with the derivation of the brewster’s angle since it is very important and many theoretical as well as numerical questions are based upon this concept.
The glare of sunlight from the reflection of water is due to the polarized nature of the light reaching our eyes. If polarized sunglasses are used, the glare can be reduced since the polarized sunglasses only allow light of a certain polarization to enter and minimize the glare. This technology is the reason why authentic polarized sunglasses are so expensive.