
State Kirchhoff’s law for an electrical network. Using these laws, deduce the condition for balance in a wheatstone bridge.
Answer
515.4k+ views
6 likes
- Hint – In order to solve this question, firstly we will understand the Kirchhoff’s laws i.e. Kirchhoff’s current law and Kirchhoff’s voltage law for an electrical network. Then we will use these two laws to find the required answer.
Complete step-by-step solution -
In 1845, a German physicist, Kirchhoff developed a pair or set of rules or laws that addressed current and energy conservation within electrical circuits. These two rules are commonly known as Kirchhoff’s current law (KCL) while other law deals with the voltage sources present in a closed circuit, Kirchhoff’s voltage law (KVL).
Kirchhoff's first law or KCL states that the total current or charge entering a junction or node is exactly the same as the charge leaving the node because it has no other way to go but to exit, because no charge is lost within the node. At any intersection, the algebraic number of the currents is zero.
Kirchhoff's second law, or KVL, states that the total voltage around the loop is equal to the sum of all the voltage drops within the same loop in any closed loop network. Inside the loop the algebraic sum of all voltages must be equal to zero.
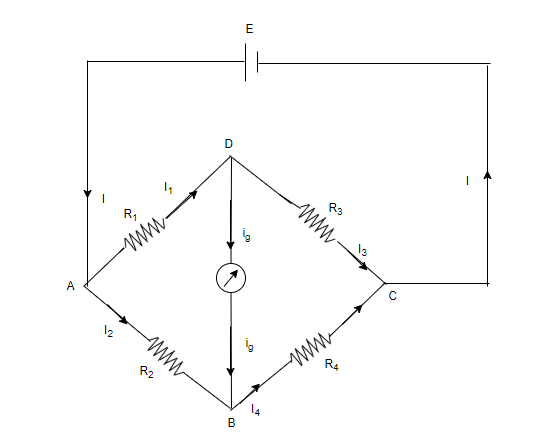
Wheatstone bridge: Wheatstone’s bridge circuit consists of four resistances
Now applying Kirchhoff’s first law-
At the junction D,
At the junction B,
Applying Kirchhoff’s second law to the closed path ADBA-
When the galvanometer shows zero deflection the points D and B are at the same potential,
So
Substituting this value in 1, 2, 3 and 4-
Dividing 7 by 8,
Wheatstone’s bridge principle:
Note- While solving this question, we must know that the Kirchhoff’s current law or KCL is also known as junction law and Kirchhoff’s voltage law or KVL is also known as loop law, so that it is beneficial to solve similar kinds of questions.
Complete step-by-step solution -

In 1845, a German physicist, Kirchhoff developed a pair or set of rules or laws that addressed current and energy conservation within electrical circuits. These two rules are commonly known as Kirchhoff’s current law (KCL) while other law deals with the voltage sources present in a closed circuit, Kirchhoff’s voltage law (KVL).
Kirchhoff's first law or KCL states that the total current or charge entering a junction or node is exactly the same as the charge leaving the node because it has no other way to go but to exit, because no charge is lost within the node. At any intersection, the algebraic number of the currents is zero.
Kirchhoff's second law, or KVL, states that the total voltage around the loop is equal to the sum of all the voltage drops within the same loop in any closed loop network. Inside the loop the algebraic sum of all voltages must be equal to zero.
Wheatstone bridge: Wheatstone’s bridge circuit consists of four resistances
Now applying Kirchhoff’s first law-
At the junction D,
At the junction B,
Applying Kirchhoff’s second law to the closed path ADBA-
When the galvanometer shows zero deflection the points D and B are at the same potential,
So
Substituting this value in 1, 2, 3 and 4-
Dividing 7 by 8,
Wheatstone’s bridge principle:
Note- While solving this question, we must know that the Kirchhoff’s current law or KCL is also known as junction law and Kirchhoff’s voltage law or KVL is also known as loop law, so that it is beneficial to solve similar kinds of questions.
Recently Updated Pages
Master Class 9 General Knowledge: Engaging Questions & Answers for Success

Master Class 9 English: Engaging Questions & Answers for Success

Master Class 9 Science: Engaging Questions & Answers for Success

Master Class 9 Social Science: Engaging Questions & Answers for Success

Master Class 9 Maths: Engaging Questions & Answers for Success

Class 9 Question and Answer - Your Ultimate Solutions Guide

Trending doubts
Give 10 examples of unisexual and bisexual flowers

Draw a labelled sketch of the human eye class 12 physics CBSE

Differentiate between homogeneous and heterogeneous class 12 chemistry CBSE

Differentiate between insitu conservation and exsitu class 12 biology CBSE

What are the major means of transport Explain each class 12 social science CBSE

a Tabulate the differences in the characteristics of class 12 chemistry CBSE




