
State Right hand thumb rule and fleming's left-hand rule.
The ratio of magnetic moment when two rectangular coils in constant magnetic field B is 4:3 which makes angle
Answer
493.8k+ views
Hint: The torque produced in a current carrying coil in the presence of magnetic field is given by:
Where, N is the no. of coils
And A is the area of the coil.
M is the magnetic moment of the coil
B is the strength of magnetic field lines passing through it.
And
Here, in the given question, the magnetic field is constant for both the coils.
Hence, the ratio of the two-torque produced will be given by:
Putting the values, we will get the answer.
Complete step by step answer:
Right hand thumb rule: According to the right hand thumb rule, if we imagine holding a current carrying conductor in our right hand so that the thumb points in the direction of current, then the direction in which fingers curl the wire will give the direction of magnetic field lines.

Fleming’s left-hand rule: According to Fleming’s left hand rule, if we stretch our thumb, forefinger and the middle finger of our left hand such that they are mutually perpendicular to each other and if the fore finger points in the direction of magnetic field and the middle finger in the direction of current, then the thumb will point in the direction of motion or force acting on the conductor.
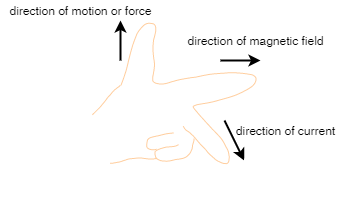
Let us assume rectangular coils, coil 1 and 2 respectively.
In the question it is given that the ratio of the magnetic moments of the coil 1 and 2 is 4:3.
It is also given that the direction of the area vector in the two coils makes an angle of
The magnetic moment produced in a coil due to current is given by:
Where, N is the no. of coils
And A is the area of the coil.
Now, the torque produced in a current carrying coil in the presence of magnetic field is given by:
Where, M is the magnetic moment of the coil
B is the strength of magnetic field lines passing through it.
And
Magnetic field is constant for both the coils.
So, Torque produced in coil 1 is:
Similarly,
The ratio of two torque produced will be:
Note:
The general formula for torque produced in a current carrying coil in the presence of magnetic field is given by:
If M and B are constant then,
So, it is maximum when,
It means if the area vector of the coil is perpendicular to the magnetic field (coil is in the plane of magnetic field) then torque would be maximum.
And torque is minimum when:
It means if the area vector of the coil is parallel to the magnetic field (coil is in perpendicular plane to magnetic field) then torque would be minimal.
Where, N is the no. of coils
And A is the area of the coil.
M is the magnetic moment of the coil
B is the strength of magnetic field lines passing through it.
And
Here, in the given question, the magnetic field is constant for both the coils.
Hence, the ratio of the two-torque produced will be given by:
Putting the values, we will get the answer.
Complete step by step answer:
Right hand thumb rule: According to the right hand thumb rule, if we imagine holding a current carrying conductor in our right hand so that the thumb points in the direction of current, then the direction in which fingers curl the wire will give the direction of magnetic field lines.

Fleming’s left-hand rule: According to Fleming’s left hand rule, if we stretch our thumb, forefinger and the middle finger of our left hand such that they are mutually perpendicular to each other and if the fore finger points in the direction of magnetic field and the middle finger in the direction of current, then the thumb will point in the direction of motion or force acting on the conductor.

Let us assume rectangular coils, coil 1 and 2 respectively.
In the question it is given that the ratio of the magnetic moments of the coil 1 and 2 is 4:3.
It is also given that the direction of the area vector in the two coils makes an angle of
The magnetic moment produced in a coil due to current is given by:
Where, N is the no. of coils
And A is the area of the coil.
Now, the torque produced in a current carrying coil in the presence of magnetic field is given by:
Where, M is the magnetic moment of the coil
B is the strength of magnetic field lines passing through it.
And
Magnetic field is constant for both the coils.
So, Torque produced in coil 1 is:
Similarly,
The ratio of two torque produced will be:
Note:
The general formula for torque produced in a current carrying coil in the presence of magnetic field is given by:
If M and B are constant then,
So, it is maximum when,
It means if the area vector of the coil is perpendicular to the magnetic field (coil is in the plane of magnetic field) then torque would be maximum.
And torque is minimum when:
It means if the area vector of the coil is parallel to the magnetic field (coil is in perpendicular plane to magnetic field) then torque would be minimal.
Latest Vedantu courses for you
Grade 10 | CBSE | SCHOOL | English
Vedantu 10 CBSE Pro Course - (2025-26)
School Full course for CBSE students
₹37,300 per year
Recently Updated Pages
Master Class 12 Business Studies: Engaging Questions & Answers for Success

Master Class 12 English: Engaging Questions & Answers for Success

Master Class 12 Social Science: Engaging Questions & Answers for Success

Master Class 12 Chemistry: Engaging Questions & Answers for Success

Class 12 Question and Answer - Your Ultimate Solutions Guide

Master Class 11 Economics: Engaging Questions & Answers for Success

Trending doubts
Draw a labelled sketch of the human eye class 12 physics CBSE

a Tabulate the differences in the characteristics of class 12 chemistry CBSE

Which one of the following is a true fish A Jellyfish class 12 biology CBSE

Why is the cell called the structural and functional class 12 biology CBSE

Differentiate between homogeneous and heterogeneous class 12 chemistry CBSE

Write the difference between solid liquid and gas class 12 chemistry CBSE




