
State the working principle of Potentiometer. Explain with the help of circuit diagram, how the potentiometer is used to determine the internal resistance of the given primary cell. In a potentiometer arrangement, a cell of emf
Answer
441.8k+ views
Hint: Potentiometer is a three-terminal resistor, which produces a voltage divider, through sliding or rolling contact.
Formula used:
Complete step-by-step answer:
Potentiometer is a three-terminal resistor, which produces a voltage divider, through sliding or rolling contact. It works on the principle that potential across the wire depends on the length of the wire, which has uniform cross-sectional area and constant current flowing through it. It can be used to measure the internal resistance of the primary cell.
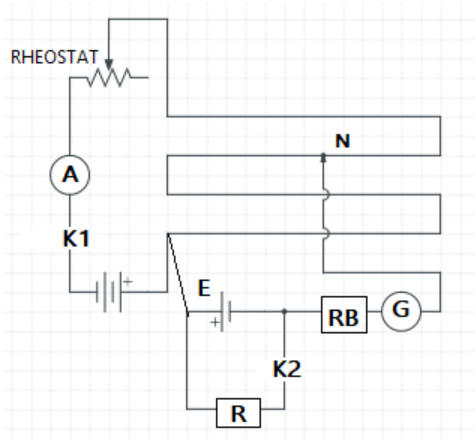
Connections are made as given in the diagram.
We know,
Also
For any potentiometer
Then, according to the principle,
Here
Then
When the plug out the
Thus
Using the given, emf of cell=
Hence the emf of the unknown is 2.25 V.
Note: Clearly understand the difference between what happens when
Formula used:
Complete step-by-step answer:
Potentiometer is a three-terminal resistor, which produces a voltage divider, through sliding or rolling contact. It works on the principle that potential across the wire depends on the length of the wire, which has uniform cross-sectional area and constant current flowing through it. It can be used to measure the internal resistance of the primary cell.

Connections are made as given in the diagram.
We know,
Also
For any potentiometer
Then, according to the principle,
Here
Then
When the plug out the
Thus
Using the given, emf of cell=
Hence the emf of the unknown is 2.25 V.
Note: Clearly understand the difference between what happens when
Recently Updated Pages
Master Class 12 Business Studies: Engaging Questions & Answers for Success

Master Class 12 English: Engaging Questions & Answers for Success

Master Class 12 Social Science: Engaging Questions & Answers for Success

Master Class 12 Chemistry: Engaging Questions & Answers for Success

Class 12 Question and Answer - Your Ultimate Solutions Guide

Master Class 11 Economics: Engaging Questions & Answers for Success

Trending doubts
Draw a labelled sketch of the human eye class 12 physics CBSE

a Tabulate the differences in the characteristics of class 12 chemistry CBSE

Which one of the following is a true fish A Jellyfish class 12 biology CBSE

Why is the cell called the structural and functional class 12 biology CBSE

Differentiate between homogeneous and heterogeneous class 12 chemistry CBSE

Write the difference between solid liquid and gas class 12 chemistry CBSE




