Question

STATEMENT-1: For an observer looking out through the window of a fast-moving train, the nearby objects appear to move in the opposite direction to the train, while the distant objects appear to be stationary.
STATEMENT-2: If the observer and the object are moving at velocities \[\overrightarrow {{{\text{V}}_{\text{1}}}} {\text{and}} \overrightarrow {{{\text{V}}_{\text{2}}}} \] respectively with reference to a laboratory frame, the velocity of the object with respect to the observer is \[\overrightarrow {{{\text{V}}_{\text{2}}}} {\text{ }}{\text{ - }}\overrightarrow {{{\text{V}}_{\text{1}}}} \] ​.

(A) STATEMENT-1 is True, STATEMENT-2 is True; STATEMENT-2 is a correct explanation for STATEMENT-1
(B) STATEMENT-1 is True, STATEMENT-2 is True; STATEMENT-2 is NOT a correct explanation for STATEMENT-1
(C) STATEMENT -1 is True, STATEMENT-2 is False
(D) STATEMENT -1 is False, STATEMENT-2 is True

Answer 1

Hint: The relative velocity of A w.r.t B is given by: \[\overrightarrow {{V_{AB}}} = \overrightarrow {{V_A}} - \overrightarrow {{V_B}} \] .
Hence when an observer in a train observes an object outside, the relative velocity of the object w.r.t to the observer comes out to be opposite to the motion of the observer. Hence, it appears to move backwards. As to why closer objects appear to move faster and distant objects appear to move very slowly or nearly stationary is due to the phenomena how much faster the angle subtended on our eyes by the object changes. For closer objects it changes rapidly, while for farther objects it changes very slowly.

Complete step by step answer:

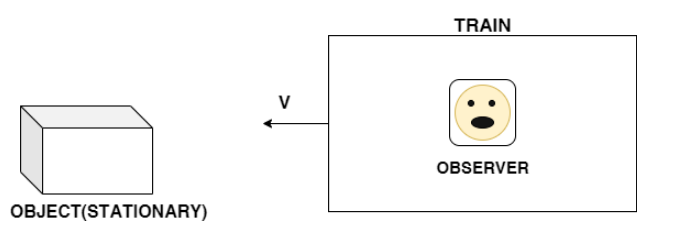
Let us take an example of a train moving in left direction with a velocity
 $\overrightarrow {{V_T}} = - v$( assuming negative sign for left and positive for right).
And the object be stationary i.e. $\overrightarrow {{V_O}} = 0$ .
Now, the relative velocity of the object with respect to the train will be given as:
\[
\overrightarrow {{V_{OT}}} = \overrightarrow {{V_O}} - \overrightarrow {{V_T}} \\
\Rightarrow \overrightarrow {{V_{OT}}} = 0 - \left( { - v} \right) = + v \\
 \]
Hence, the object will appear to move backward with velocity v to the observer.
And also, if object is not stationary and has an initial velocity $\overrightarrow {{V_1}} $ and observer has a velocity $\overrightarrow {{V_2}} $ then the relative velocity of object with respect to observer will be given as:
\[\overrightarrow {{V_{21}}} = \overrightarrow {{V_2}} - \overrightarrow {{V_1}} \]
Hence, both the statements 1 and 2 are true; but the statement 2 is not the correct explanation for the assertion 1.
And the reason why closer objects appear to move faster to the observer in train and distant objects appear to move slow or stationary is due to the fact that the line of sight for the object closer to the train(observer) is very small and therefore, they move very fast while, objects like trees or mountains that are very far away appear to move very slowly or approximately stationary because of the large line of sight for the farther objects.

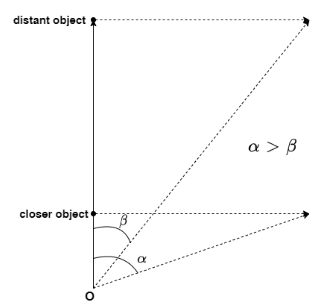
How fast an object appears to move depends upon how fast the angle subtended by it on our eye’s changes, which makes us realize that the object has displaced from its position. For closer objects the change in angle is very large while for distant objects it's very small or negligible.

Note: For a very distant object like moon, sun, star etc. It appears like they are stationary or following us as we are moving. It is due to the same phenomena as explained above. The change in angle for a very far object like the moon is very negligible $\left( {\beta \approx 0} \right)$that our eye doesn’t perceive any change in the line of sight. Moreover, as the closer objects like trees, buildings etc. appear to move backwards due to the smaller line of sight that it enhances our perception that the moon is keeping with us. This phenomena is called parallax.