Question

Sum of all interior angles of a parallelogram is
a) \[{180^\circ }\]
b) \[{360^\circ }\]
c) \[{540^\circ }\]
d) \[{240^\circ }\]

Answer 1

Hint: A parallelogram is a polygon having four sides. Since we know that all interior angles on the same side of the transversal are supplementary. We can use this property to get the sum of all the interior angles of a parallelogram. Same way we can use a formula given as \[\left( {n - 2} \right) \times {180^\circ }\]. With the help of the given formula we can find the sum of all interior angles of any polygon.
Formula used: Sum of all interior angles of a polygon is given as \[\left( {n - 2} \right) \times {180^\circ }\]. Here \[n\] is the number of sides a polygon has.

Complete step-by-step solution:
Here we are required to find the sum of all interior angles of a parallelogram. We are going to find by using both the formula of sum of all interior angles of polygon and supplementary angles property.
By formula method, we know that the sum of all interior angles of a polygon is given as \[\left( {n - 2} \right) \times {180^\circ }\]. Here \[n\] is the number of sides a polygon has.
Now we know that a parallelogram is a polygon having four sides, so here \[n = 4\]. Putting this in \[\left( {n - 2} \right) \times {180^\circ }\].
\[
   \Rightarrow \left( {4 - 2} \right) \times {180^\circ } \\
   \Rightarrow 2 \times {180^\circ } \\
   \Rightarrow {360^\circ } \]
So, the sum of all interior angles of a parallelogram is \[{360^\circ }\].
Now, using supplementary angles property,
We know that all interior angles on the same side of the transversal are supplementary.

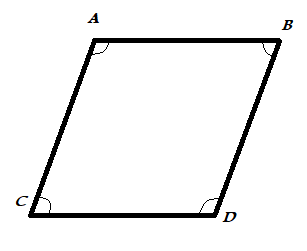
So, \[\angle A + \angle B = {180^\circ }\] and \[\angle C + \angle D = {180^\circ }\].
Now we take sum of all the angles,
\[\angle A + \angle B + \angle C + \angle D = {180^\circ } + {180^\circ }\]
\[ \Rightarrow \angle A + \angle B + \angle C + \angle D = {360^\circ }\]
So by this method also, we get to sum all interior angles of a parallelogram as \[{360^\circ }\].
Hence the answer is b) \[{360^\circ }\].

Note: It is to note that the sum of all interior angles of a polygon of four sides is \[{360^\circ }\] whether it is a square, rectangle, kite, trapezium etc. In the same way, using \[\left( {n - 2} \right) \times {180^\circ }\] we can find the sum of all the interior angles of any polygon having any number of sides. For ex. for a pentagon the sum of all the interior angles is \[\left( {5 - 2} \right) \times {180^\circ } = {540^\circ }\].