
Suppose that two cards are drawn at random from a deck of cards. Let X be the number of aces obtained. Then the value of E(X) is
\[\begin{align}
& A.\dfrac{37}{221} \\
& B.\dfrac{5}{13} \\
& C.\dfrac{1}{13} \\
& D.\dfrac{2}{13} \\
\end{align}\]
Answer
569.4k+ views
Hint: This question requires the knowledge of the number and types of cards in a deck of cards. So, we have 52 cards in total and there are 4 aces in it. Now, here we have to find the value of E(X), so we will use formula as \[\pi =E\left( X \right)=\sum\nolimits_{i=1}^{n}{={{x}_{i}}{{p}_{i}}}\] . We have to draw 2 cards and so we can have X = 0, 1 and 2. Probability can be found as favorable outcomes by total outcomes.
Complete step by step answer:
This is the probability question based on the concept of the card (here, the deck of cards means- a pack of 52 playing cards. 13 of each suit clubs, diamond, heart, and spade). i.e.
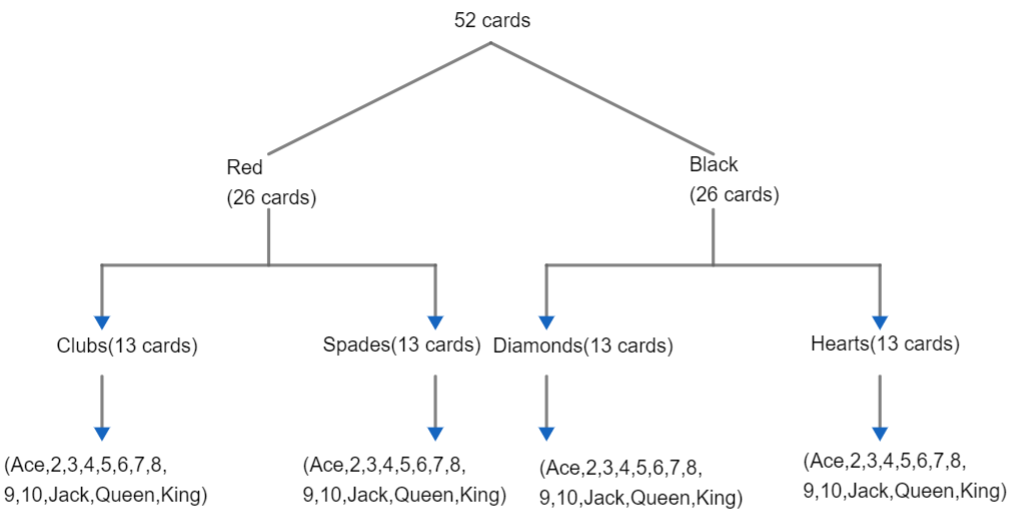
Total 12 face cards are there (jack, queen, king in each suit).
In the question given to us, it is mentioned about aces. So, we have a total of 4 aces. Here, E(X) is the expectation value. i.e.
\[\pi =E\left( X \right)=\sum\nolimits_{i=1}^{n}{={{x}_{i}}{{p}_{i}}}\]
Let X be the number of aces obtained.
According to the question, two cards are drawn. Hence, we can get 0, 1 or 2 aces.
So, the value of X is 0, 1 or 2.
We know, total number of ways to draw 2 cards out of 52 is:
\[\text{Total ways}={}^{52}{{C}_{2}}=1326\left( \because {}^{n}{{C}_{r}}=\dfrac{n!}{r!\left( n-r \right)!} \right)\]
Now, P(X=0) i.e. probability of getting 0 aces.
Number of ways to get 0 aces = Number of ways to select 2 cards out of non-ace cards.
\[\begin{align}
& \Rightarrow \text{Number of ways to select 2 cards out of }\left( \text{52}-\text{4} \right)\text{ i}.\text{e}.\text{ 48 cards} \\
& \Rightarrow {}^{\text{48}}{{\text{C}}_{\text{2}}} \\
& \Rightarrow 1128 \\
\end{align}\]
\[\begin{align}
& \text{P}\left( \text{X}=0 \right)=\dfrac{\text{Number of ways to get 0 aces}}{\text{Total number of ways}} \\
& \Rightarrow \dfrac{1128}{1326} \\
\end{align}\]
P(X=1) i.e. probability of getting 1 ace.
\[\begin{align}
& \text{Number of ways to get 1 ace}=\left( \text{Number of ways to select 1 ace out of 4 ace cards} \right)\times \\
& \left( \text{Number of ways to select 1 card from 48 non-ace cards} \right) \\
& \Rightarrow {}^{4}{{C}_{1}}\times {}^{48}{{C}_{1}} \\
& \Rightarrow 4\times 48 \\
& \Rightarrow 192 \\
\end{align}\]
\[\begin{align}
& \text{P}\left( \text{X}=1 \right)=\dfrac{\text{Number of ways to get 1 aces}}{\text{Total number of ways}} \\
& \Rightarrow \dfrac{192}{1326} \\
\end{align}\]
P(X=2) i.e. probability of getting 2 aces.
Number of ways to get 2 ace = Number of ways of selecting 2 aces out of 4 ace cards.
\[\begin{align}
& \Rightarrow {}^{4}{{C}_{2}} \\
& \Rightarrow 6 \\
\end{align}\]
\[\begin{align}
& \text{P}\left( \text{X}=2 \right)=\dfrac{\text{Number of ways to get 2 aces}}{\text{Total number of ways}} \\
& \Rightarrow \dfrac{6}{1326} \\
\end{align}\]
The probability distribution is
The expectation value E(X) is given by \[\pi =E\left( X \right)=\sum\nolimits_{i=1}^{n}{={{x}_{i}}{{p}_{i}}}\]
\[\begin{align}
& \Rightarrow \left( 0\times \dfrac{1128}{1326} \right)+\left( 1\times \dfrac{192}{1326} \right)+\left( 2\times \dfrac{6}{1326} \right) \\
& \Rightarrow 0+\dfrac{192+12}{1326} \\
& \Rightarrow \dfrac{204}{1326} \\
& \Rightarrow \dfrac{2}{13} \\
\end{align}\]
Therefore, $E\left( X \right)=\dfrac{2}{13}$ is the correct answer.
Note:
Generally, there is not a big mistake that can occur in this particular problem. But yes, there may be a little bit of error if we don't read the question carefully. Like, some students take the value of X as 0, 1, 2, 3, 4. They think that there are four aces in a deck. But in the given question, there are two cards drawn, hence, at maximum, we can draw 2 aces only.
Complete step by step answer:
This is the probability question based on the concept of the card (here, the deck of cards means- a pack of 52 playing cards. 13 of each suit clubs, diamond, heart, and spade). i.e.

Total 12 face cards are there (jack, queen, king in each suit).
In the question given to us, it is mentioned about aces. So, we have a total of 4 aces. Here, E(X) is the expectation value. i.e.
\[\pi =E\left( X \right)=\sum\nolimits_{i=1}^{n}{={{x}_{i}}{{p}_{i}}}\]
Let X be the number of aces obtained.
According to the question, two cards are drawn. Hence, we can get 0, 1 or 2 aces.
So, the value of X is 0, 1 or 2.
We know, total number of ways to draw 2 cards out of 52 is:
\[\text{Total ways}={}^{52}{{C}_{2}}=1326\left( \because {}^{n}{{C}_{r}}=\dfrac{n!}{r!\left( n-r \right)!} \right)\]
Now, P(X=0) i.e. probability of getting 0 aces.
Number of ways to get 0 aces = Number of ways to select 2 cards out of non-ace cards.
\[\begin{align}
& \Rightarrow \text{Number of ways to select 2 cards out of }\left( \text{52}-\text{4} \right)\text{ i}.\text{e}.\text{ 48 cards} \\
& \Rightarrow {}^{\text{48}}{{\text{C}}_{\text{2}}} \\
& \Rightarrow 1128 \\
\end{align}\]
\[\begin{align}
& \text{P}\left( \text{X}=0 \right)=\dfrac{\text{Number of ways to get 0 aces}}{\text{Total number of ways}} \\
& \Rightarrow \dfrac{1128}{1326} \\
\end{align}\]
P(X=1) i.e. probability of getting 1 ace.
\[\begin{align}
& \text{Number of ways to get 1 ace}=\left( \text{Number of ways to select 1 ace out of 4 ace cards} \right)\times \\
& \left( \text{Number of ways to select 1 card from 48 non-ace cards} \right) \\
& \Rightarrow {}^{4}{{C}_{1}}\times {}^{48}{{C}_{1}} \\
& \Rightarrow 4\times 48 \\
& \Rightarrow 192 \\
\end{align}\]
\[\begin{align}
& \text{P}\left( \text{X}=1 \right)=\dfrac{\text{Number of ways to get 1 aces}}{\text{Total number of ways}} \\
& \Rightarrow \dfrac{192}{1326} \\
\end{align}\]
P(X=2) i.e. probability of getting 2 aces.
Number of ways to get 2 ace = Number of ways of selecting 2 aces out of 4 ace cards.
\[\begin{align}
& \Rightarrow {}^{4}{{C}_{2}} \\
& \Rightarrow 6 \\
\end{align}\]
\[\begin{align}
& \text{P}\left( \text{X}=2 \right)=\dfrac{\text{Number of ways to get 2 aces}}{\text{Total number of ways}} \\
& \Rightarrow \dfrac{6}{1326} \\
\end{align}\]
The probability distribution is
| X | 0 | 1 | 2 |
| P(X) | $\dfrac{1128}{1326}$ | $\dfrac{192}{1326}$ | $\dfrac{6}{1326}$ |
The expectation value E(X) is given by \[\pi =E\left( X \right)=\sum\nolimits_{i=1}^{n}{={{x}_{i}}{{p}_{i}}}\]
\[\begin{align}
& \Rightarrow \left( 0\times \dfrac{1128}{1326} \right)+\left( 1\times \dfrac{192}{1326} \right)+\left( 2\times \dfrac{6}{1326} \right) \\
& \Rightarrow 0+\dfrac{192+12}{1326} \\
& \Rightarrow \dfrac{204}{1326} \\
& \Rightarrow \dfrac{2}{13} \\
\end{align}\]
Therefore, $E\left( X \right)=\dfrac{2}{13}$ is the correct answer.
Note:
Generally, there is not a big mistake that can occur in this particular problem. But yes, there may be a little bit of error if we don't read the question carefully. Like, some students take the value of X as 0, 1, 2, 3, 4. They think that there are four aces in a deck. But in the given question, there are two cards drawn, hence, at maximum, we can draw 2 aces only.
Recently Updated Pages
Master Class 12 Business Studies: Engaging Questions & Answers for Success

Master Class 12 Economics: Engaging Questions & Answers for Success

Master Class 12 English: Engaging Questions & Answers for Success

Master Class 12 Maths: Engaging Questions & Answers for Success

Master Class 12 Social Science: Engaging Questions & Answers for Success

Master Class 12 Chemistry: Engaging Questions & Answers for Success

Trending doubts
Who was the first woman to receive Bharat Ratna?

Write a letter to the principal requesting him to grant class 10 english CBSE

Why is there a time difference of about 5 hours between class 10 social science CBSE

What is the median of the first 10 natural numbers class 10 maths CBSE

The Equation xxx + 2 is Satisfied when x is Equal to Class 10 Maths

Discuss the main reasons for poverty in India




