Question

Surface charge density of a cylinder of length 44m is $17.7\mu C/m{m^2}$. If the cylinder is placed in air then the electric field at a point just outside the cylinder is:
A. $2 \times {10^{12}}V/m$
B. $2 \times {10^6}V/m$
C. $8.85 \times {10^{ - 12}}$
D. $2 \times {10^{ - 6}}V/m$

Answer 1

Hint: In order to find the electric field we use integration usually. But if integration over the body becomes complicated then we use a simple law called gauss law in order to find out the electric field due to the charged body. Integration for non uniform shaped bodies will be difficult. Then gauss law might help. We solve this problem using gauss law.

Formula used:
$\int {E.dA} = \dfrac{{{q_{in}}}}{{{\varepsilon _0}}}$

Complete step by step solution:
There are some limitations where we can apply gauss law. In order to apply gauss law we will consider a gaussian surface. Now that gaussian surface should not pass through the point charge or discrete charge. It can pass through continuous charge. The electric field on that gaussian surface will be due to the charges inside and outside the gaussian surface, but the charge we take for the application of the gauss law should be the charge inside the gaussian surface.
We can take any gaussian surface. But if we need to find an electric field at the point on gaussian surface then the conditions to be followed is, electric field but be same everywhere on the gaussian surface and electric field must be either parallel or perpendicular to gaussian surface and the gaussian surface must be symmetrical.
Gauss law will be
$\int {E.dA} = \dfrac{{{q_{in}}}}{{{\varepsilon _0}}}$
For the cylinder given, let the cross section area be A and surface charge density is sigma and ${q_{in}}$ is charged inside the cylinder.
$\sigma = \dfrac{{{q_{in}}}}{A}$

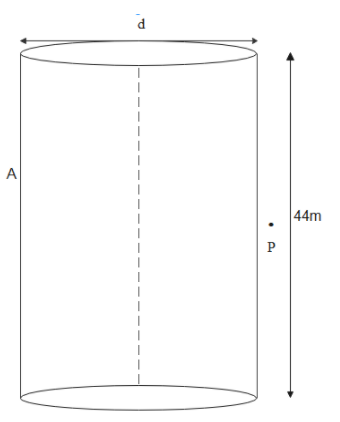
From the figure above the electric field at point P can be found by passing the gaussian cylinder through P and applying gauss law to it.
$\eqalign{
  & \int {E.dA} = \dfrac{{{q_{in}}}}{{{\varepsilon _0}}} \cr
  & \Rightarrow E.A = \dfrac{{{q_{in}}}}{{{\varepsilon _0}}} \cr
  & \Rightarrow E = \dfrac{{\left( {\dfrac{{{q_{in}}}}{A}} \right)}}{{{\varepsilon _0}}} \cr
  & \Rightarrow E = \dfrac{\sigma }{{{\varepsilon _0}}} \cr
  & \Rightarrow E = \dfrac{{\dfrac{{17.7 \times {{10}^{ - 6}}}}{{{{10}^{ - 6}}}}C/{m^2}}}{{8.85 \times {{10}^{ - 12}}}} \cr
  & \therefore E = 2 \times {10^{12}}V/m \cr} $

Hence option A will be the answer.

Note:
We can consider the gaussian surface of any shape. But in order to calculate the electric field very easily by avoiding the long integrations we will generally select a symmetrical gaussian surface. We find the electric field due to long wire and long conducting sheet by using the gauss law. There we choose different gaussian surfaces.