Question

How tall is a bridge if a 6 foot tall person standing 100 feet away can see the top of the bridge at an angle of 30 degrees to the horizon?

Answer 1

Hint:The above given question is a simple mathematical trigonometric word problem.
In order to express a mathematical problem explained in words we have to take all the relevant and important information mentioned in the word problem and represent it in a much easier way like an equation.
So by using the above definition and techniques we can solve the given question.

Complete step by step solution:
Given statement:
$
6{\text{ foot tall person standing }}100{\text{ feet away:}}\left( i \right) \\
{\text{At an angle }}{30^ \circ }{\text{to horizon he can see the top of the bridge:}}\left( {ii} \right)
\\
$
Now using the above two statements we have to find the height of the bridge.
Let’s assume that the eye level of the person to be at\[6\;{\text{feet}}\].
Now let the height of the bridge be$h$, also let the height $h$and the distance $100$be the legs of a right angle:
So now let’s construct a right angled triangle from the given information.
Such that we can draw as below:

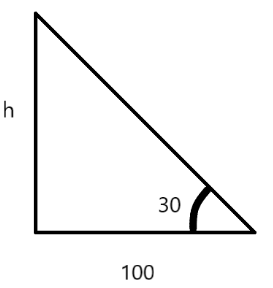
Now we need to find$h$, for that let’s use some basic trigonometric properties. We know that:
\[\tan \theta = \dfrac{{{\text{opposite}}\;{\text{side}}}}{{{\text{adjacent}}\;{\text{side}}}}\]
Here $\theta = {30^ \circ }$and also \[\tan {30^ \circ } = \dfrac{1}{{\sqrt 3 }}.............................\left(
{iii} \right)\]
Also from the given right angled triangle we can write:

\[\tan {30^ \circ } = \dfrac{h}{{100}} = \dfrac{1}{{\sqrt 3 }}.................\left( {iv} \right)\]
On simplifying (iv):
$h = \dfrac{{100}}{{\sqrt 3 }} = \dfrac{{100\sqrt 3 }}{3}$
Now we got $h$as$\dfrac{{100\sqrt 3 }}{3}$. But here we have assumed the eye level of the person to be at\[6\;{\text{feet}}\], so by also considering the height of the person since ${30^ \circ }$is measured relatively, we can say that the height of the bridge would be:$6 + \dfrac{{100\sqrt 3 }}{3}$
Therefore the bridge would be $6 + \dfrac{{100\sqrt 3 }}{3}$tall.


Note:
While solving a word problem after representing it in the symbolic form we have to try to eliminate various variables represented using equations by rearranging terms, using basic arithmetic operations and substitutions. Eventually we would be able to solve the question.
Some basic trigonometric identities are:
\[

\sin \theta = \dfrac{{{\text{opposite}}\;{\text{side}}}}{{{\text{hypotenuse}}}} \\
\cos \theta = \dfrac{{{\text{adjacent}}\;{\text{side}}}}{{{\text{hypotenuse}}}} \\
\tan \theta = \dfrac{{{\text{opposite}}\;{\text{side}}}}{{{\text{adjacent}}\;{\text{side}}}} \\
\]