Question

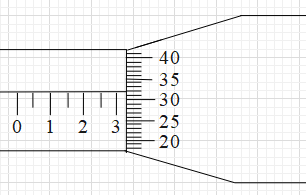
The accompanying diagram represents a screw gauge. The circular scale is divided into 50 divisions and the linear scale is divided into millimeters. If the screw advances by 1mm when the circular scale makes 2 complete revolutions, the least count of the instrument and the reading of the instrument in figure are:

A. 0.01mm, 3.82mm
B. 0.01mm, 4.82mm
C. 0.02mm, 3.82mm
D. 0.05mm, 3.82mm

Answer 1

Hint: Calculate the pitch of the screw gauge with the help of the given information. Then divide the pitch by the number of circular scale divisions to find the least count of the instrument. To calculate the reading of the measurement shown, use the formula for the reading of a screw gauge.

Formula used: $p=\dfrac{\text{length moved}}{\text{revolutions needed}}$
$LC=\dfrac{p}{N}$
$l=LSR+(LC\times CSR)$

Complete step by step answer:
Let us first calculate the pitch of the screw gauge. The pitch of a screw gauge is defined as the ratio of the length moved on the linear scale to the number of revolutions of the circular scale needed for this movement.
i.e. $p=\dfrac{\text{length moved}}{\text{revolutions needed}}$.
 It is given that when the circular scale makes 2 complete revolutions, the screw moves for 1mm.
Therefore, $p=\dfrac{1}{2}=0.5mm$.
The least count of a screw gauge is equal to the pitch divided by the number of divisions on the circular scale.
i.e. $LC=\dfrac{p}{N}$, LC is the least count and N is the number of divisions on the circular scale.
Here, N = 50.
$\Rightarrow LC=\dfrac{p}{N}=\dfrac{0.5}{50}=0.01mm$.
Therefore, the least count of the given instrument is 0.01mm.
The reading of a screw gauge is given as $l=LSR+(LC\times CSR)$ …. (i).
Here, LSR is the linear scale reading and CSR is the circular scale reading.
From the given figure of the measurement, we get that LSR = 3mm and CSR = 32.
Substitute the values of LSR and CSR in equation (i).
$l=3+(0.01\times 32)=3+0.32=3.32mm$.
This means that the reading of the instrument is 3.32mm.

So, the correct answer is “Option A”.

Note: Sometimes the instrument may have an instrumental error.
Actually, when the linear scale reading is zero, the circular scale must be zero. However, sometimes the circular scale reading may not show zero. Therefore, there will be an error in the final reading. Hence, the error must be corrected.