
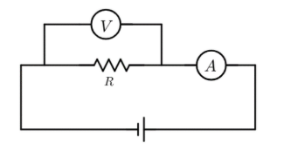
The actual value of resistance R shown in the figure is

Answer
473.4k+ views
Hint: First determine the measured effective resistance value of the circuit given that it is
Formula Used:
Effective resistance of two resistors in parallel:
Complete Step-by-Step Solution:
We are given that the actual value of resistance R is
But the measured value is
We are given that this reduction in the measured value is due to the internal resistance
But we know that the effective resistance of the setup is the measured value of the resistance, i.e.,
Therefore, the internal resistance of the voltmeter is found to be
Note:
Remember that a series circuit is a voltage divider whereas a parallel circuit is a current divider. We add up all the resistances in a series circuit because the resistances are arranged in such a way that the current has only one path to take. However, when resistances are connected in parallel, there are multiple paths for the current to pass through but have the same potential difference across them. This results in a net resistance that is lower than any of the individual resistances.
This is also the same reason why the voltmeter might read a lower voltage if a resistance is connected in parallel to it. This is because the internal resistance of the voltmeter is generally very high and if a relatively low resistance is introduced in a parallel branch, most of the current gets diverted to the path of least resistance and the voltmeter receives relatively lesser current and is thus able to process it and show a lesser voltage.
Formula Used:
Effective resistance of two resistors in parallel:
Complete Step-by-Step Solution:
We are given that the actual value of resistance R is
But the measured value is
We are given that this reduction in the measured value is due to the internal resistance
But we know that the effective resistance of the setup is the measured value of the resistance, i.e.,
Therefore, the internal resistance of the voltmeter is found to be
Note:
Remember that a series circuit is a voltage divider whereas a parallel circuit is a current divider. We add up all the resistances in a series circuit because the resistances are arranged in such a way that the current has only one path to take. However, when resistances are connected in parallel, there are multiple paths for the current to pass through but have the same potential difference across them. This results in a net resistance that is lower than any of the individual resistances.
This is also the same reason why the voltmeter might read a lower voltage if a resistance is connected in parallel to it. This is because the internal resistance of the voltmeter is generally very high and if a relatively low resistance is introduced in a parallel branch, most of the current gets diverted to the path of least resistance and the voltmeter receives relatively lesser current and is thus able to process it and show a lesser voltage.
Recently Updated Pages
Master Class 12 Business Studies: Engaging Questions & Answers for Success

Master Class 12 English: Engaging Questions & Answers for Success

Master Class 12 Social Science: Engaging Questions & Answers for Success

Master Class 12 Chemistry: Engaging Questions & Answers for Success

Class 12 Question and Answer - Your Ultimate Solutions Guide

Master Class 11 Economics: Engaging Questions & Answers for Success

Trending doubts
Draw a labelled sketch of the human eye class 12 physics CBSE

a Tabulate the differences in the characteristics of class 12 chemistry CBSE

Which one of the following is a true fish A Jellyfish class 12 biology CBSE

Why is the cell called the structural and functional class 12 biology CBSE

Differentiate between homogeneous and heterogeneous class 12 chemistry CBSE

Write the difference between solid liquid and gas class 12 chemistry CBSE




