Question

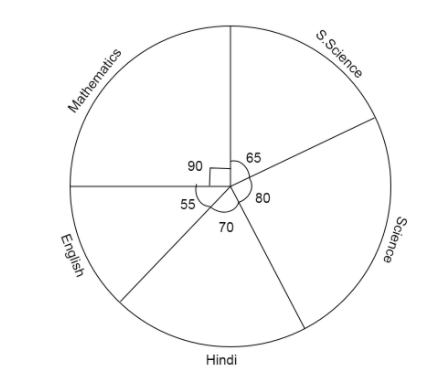
The adjoining pie chart gives the marks scored in an examination by a student in Hindi, English, Mathematics, Social science and Science. If the total marks obtained by the students were 540, answer the following questions:
(i) In which subject did the student score 105 marks? So, for 105 marks, what is the central angle?
(ii) How many more marks were obtained by the student in Mathematics than in Hindi?
(iii) Examine whether the sum of the marks obtained in Social science and Mathematics is more than that in Science and Hindi.

Answer 1

Hint: Here we assume that in a pi diagram \[{360^ \circ }\] is the total angle representing the total number of marks. We use a unitary method to find the value of marks of each subject when we are given the total angle and measure of angle for each subject. We first calculate the central angle from the first part and check for which subject it matches the given angle in the pie chart. Similarly for later parts we use the formula of central angle.
* Unitary method helps us to find the value of multiple units if we are given the value of a single unit by multiplying the value of a single unit to the number of multiple units.
* A pie-chart is a kind of chart in the shape of a circle, where the sectors depict the amount or quantity of each kind of object. Each sector represents a proportion of the whole.

Complete step-by-step solution:
In a pi diagram the total angle is \[{360^ \circ }\].
Let us assume that \[{360^ \circ }\]represents the total number of marks i.e. 540
We find the central angle for 1 cycle using unitary method:
Since, 540 marks have central angle \[ = {360^ \circ }\]
\[ \Rightarrow \]1 mark will have central angle \[ = \dfrac{{{{360}^ \circ }}}{{540}}\]
So for any marks, say x the central angle will be \[ = \dfrac{{{{360}^ \circ }}}{{540}} \times x\]
On solving the fraction we get;
\[ \Rightarrow \]Central angle for x marks \[ = {(\dfrac{2}{3})^ \circ }\]..............… (1)
(i) We are given the marks scored by students in a subject of 105. We have to calculate the central angle for this subject and check using the given pie chart which subject is being talked about.
Number of marks obtained by student \[ = 105\]
We use the formula from equation (1) to find the central angle in pi diagram
\[ \Rightarrow \]Central angle for 150 marks\[ = {(105 \times \dfrac{2}{3})^ \circ } = {70^ \circ }\]
Since the pie chart gives marks of student in Hindi with angle \[{70^ \circ }\]
\[\therefore \]Student obtained 105 marks in Hindi with central angle as \[{70^ \circ }\]
(ii) We calculate marks obtained by students in mathematics and use the answer from part (i) and calculate the difference between the marks.
We know central angle for x marks \[ = {(\dfrac{2}{3})^ \circ }\]
Also we are given central angle for mathematics is \[{90^ \circ }\]
Let marks in mathematics is ‘y’
\[ \Rightarrow \]Central angle for ‘y’ marks\[ = {(y \times \dfrac{2}{3})^ \circ } = {90^ \circ }\]
\[ \Rightarrow {(y \times \dfrac{2}{3})^ \circ } = {90^ \circ }\]
Cross multiply all the values except y to RHS of the equation
\[ \Rightarrow y = {90^ \circ } \times \dfrac{3}{2}\]
\[ \Rightarrow y = 135\]
So, marks obtained in mathematics are 135 and from part (i) marks in Hindi were 105.
\[ \Rightarrow \]Difference in marks in mathematics and Hindi \[ = 135 - 105 = 30\]
\[\therefore \]Student scored 30 more marks in mathematics than in Hindi
(iii) We calculate the marks obtained in Social science, Mathematics, Science and Hindi and take the sum of given pairs and calculate the difference between the pairs.
Social science and mathematics:
We know marks obtained in mathematics are 135.
We know central angle for x marks \[ = {(\dfrac{2}{3})^ \circ }\]
Also we are given central angle for Social science is \[{65^ \circ }\]
Let marks in mathematics is ‘z’
\[ \Rightarrow \]Central angle for ‘z’ marks\[ = {(z \times \dfrac{2}{3})^ \circ } = {65^ \circ }\]
\[ \Rightarrow {(z \times \dfrac{2}{3})^ \circ } = {65^ \circ }\]
Cross multiply all the values except y to RHS of the equation
\[ \Rightarrow z = {65^ \circ } \times \dfrac{3}{2}\]
\[ \Rightarrow z = 97.5\]
So, marks obtained in Social science are 97.5
Total marks obtained in Social science and mathematics \[ = 97.5 + 135 = 232.5\]
Sum of marks in Social science and mathematics is 232.5………………..… (2)
Science and Hindi:
We know marks obtained in Hindi are 105.
We know central angle for x marks \[ = {(\dfrac{2}{3})^ \circ }\]
Also we are given central angle for science is \[{80^ \circ }\]
Let marks in mathematics is ‘p’
\[ \Rightarrow \]Central angle for ‘p’ marks\[ = {(p \times \dfrac{2}{3})^ \circ } = {80^ \circ }\]
\[ \Rightarrow {(p \times \dfrac{2}{3})^ \circ } = {80^ \circ }\]
Cross multiply all the values except y to RHS of the equation
\[ \Rightarrow p = {80^ \circ } \times \dfrac{3}{2}\]
\[ \Rightarrow p = 120\]
So, marks obtained in science are 120
Total marks obtained in science and Hindi \[ = 120 + 105 = 225\]
Sum of marks in science and Hindi is 225 ……………….… (3)
Since \[232.5 > 225\]
So, the sum of the marks obtained in Social science and Mathematics is more than that in Science and Hindi.

Note: Many students make mistakes while cross multiplying the values while solving for the value of marks. Keep in mind we take reciprocal of the fraction when we cross multiply the terms of fraction from one side of the equation to another.