Question

The angle of elevation of a tower from a point on the same level as the foot of the tower is ${30^0}$. On advancing 150 meters towards the foot of the tower, the angle of elevation of the tower becomes ${60^0}$. Show that the height of the tower is 129.9 meters. (Use $\sqrt 3 = 1.732$).

Answer 1

Hint- Angles of elevation are given so we find the relation between sides and angles by using some basic trigonometric properties such as $\tan \theta = \dfrac{{{\text{Height}}}}{{{\text{Base}}}}$, To reach the answer we draw the triangle for the given problem.

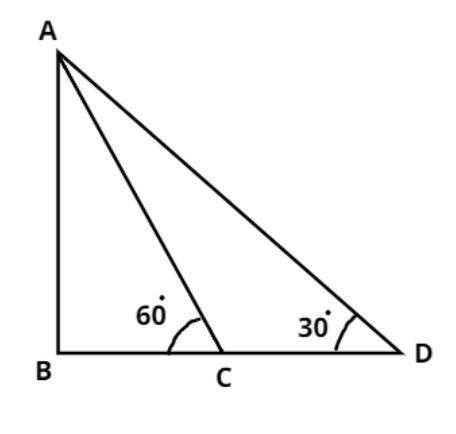
The pictorial representation of the given problem is shown above.
It is given that the angle of elevation of a tower from a point on the same level as the foot of the tower is ${30^0}$
$\therefore \angle BDA = {30^0}$
Now advancing 150 meter towards the foot of the tower, the angle of elevation of the tower becomes ${60^0}$.
$\therefore \angle BCA = {30^0},\;{\text{DC = 150m}}$
Let the height of tower is h meter
$\therefore AB = h\;{\text{m}}$
Let $BD = x{\text{ m}}$
$ \Rightarrow BC = BD - DC = \left( {x - 150} \right)m$
In triangle ABC
$\tan {60^0} = \dfrac{{{\text{Height}}}}{{{\text{Base}}}} = \dfrac{{AB}}{{BC}} = \dfrac{h}{{x - 150}}$
And we know the value of $\tan {60^0} = \sqrt 3 $
$ \Rightarrow \sqrt 3 = \dfrac{h}{{x - 150}}................\left( 1 \right)$
Now in triangle ABD
$\tan {30^0} = \dfrac{{{\text{Height}}}}{{{\text{Base}}}} = \dfrac{{AB}}{{BD}} = \dfrac{h}{x}$
And we know the value of $\tan {30^0} = \dfrac{1}{{\sqrt 3 }}$
$
   \Rightarrow \dfrac{1}{{\sqrt 3 }} = \dfrac{h}{x} \\
   \Rightarrow x = h\sqrt 3 \\
$
Now substitute the value of x in equation (1) we have
$
   \Rightarrow \sqrt 3 = \dfrac{h}{{h\sqrt 3 - 150}} \\
   \Rightarrow 3h - 150\sqrt 3 = h \\
   \Rightarrow 2h = 150\sqrt 3 \\
   \Rightarrow h = 75\sqrt 3 \\
   \Rightarrow h = 75 \times 1.732 = 129.9m \\
$
Hence Proved.

Note- whenever we face such types of questions first draw the pictorial representation of the given problem as above then apply the trigonometric identities of tan in triangles which is stated above, then according to given conditions substitute the values and simplify, we will get the required height of the tower.