Question

The angle of elevation of the top of a hill from a point is \[\alpha \]. After walking \[b\] meters towards the top up a slope inclined at an angle of \[\beta \] to the horizontal, the angle of elevation of the top becomes \[\gamma \]. Then, the height of the hill is
(A) \[\dfrac{b\sin \alpha \sin \left( \gamma -\beta \right)}{\sin \left( \gamma -\alpha \right)}\]
(B) \[\dfrac{b\sin \alpha \sin \left( \gamma -\alpha \right)}{\sin \left( \gamma -\beta \right)}\]
(C) \[\dfrac{b\sin \left( \gamma -\alpha \right)}{\sin \left( \gamma -\beta \right)}\]
(D) \[\dfrac{b\sin \left( \gamma -\beta \right)}{\sin \left( \gamma -\alpha \right)}\]

Answer 1

Hint: Assume that AB is the height of the hill and the length QC is b meters towards the top up a slope inclined at an angle of \[\beta \] to the horizontal. We know that \[\sin \theta =\dfrac{Perpendicular}{Hypotenuse}\] . Now, apply the sine ratio in \[\Delta QDC\], and \[\Delta APQ\] to obtain QD and AP. We also know the property that in any triangle, the sum of the interior two angles is equal to the corresponding exterior angle. Apply this property for \[\Delta AQR\] and get \[\angle QAR\] . We can say that \[\angle ACQ=\angle ACB-\angle QCD=\alpha -\beta \] . We know the sine formula for a triangle, \[\dfrac{a}{\sin A}=\dfrac{b}{\sin B}=\dfrac{c}{\sin C}\] . Apply this formula for \[\Delta AQC\] and get the value of AQ.

Complete step-by-step solution:
Now, solve it further and calculate AB by using \[AB=AP+PB\].
First of all, let us assume that AB is the height of the hill and the length QC is b meters towards the top up a slope inclined at an angle of \[\beta \] to the horizontal.
 

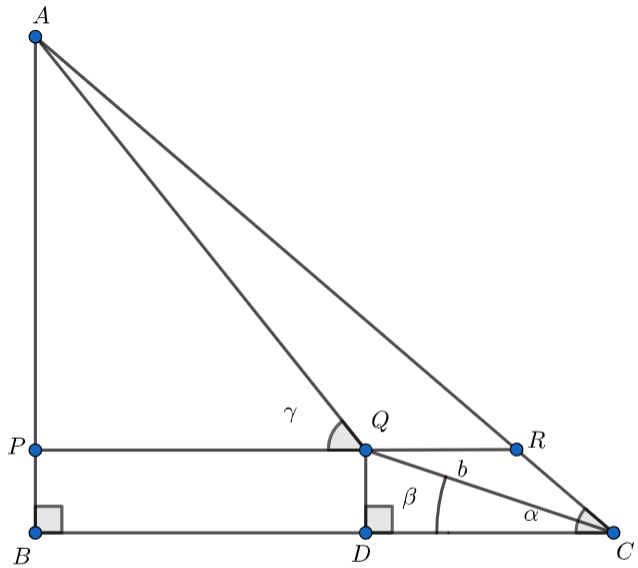
From the above figure, we can see that
The angle of elevation of the top of a hill from point C, \[\angle ACB\] = \[\alpha \] ……………………………………..(1)
 After walking a distance of b meters towards the top up a slope inclined at an angle of \[\beta \] to the horizontal,
The angle of elevation of the top of a hill from point Q, \[\angle AQP\] = \[\gamma \] ………………………………………(2)
In \[\Delta QDC\], we have
\[\angle QDC=90{}^\circ \]
\[\angle QCD=\beta \] ………………………………………….(3)
Perpendicular = QD ………………………………………..(4)
Hypotenuse = QC = \[b\] ……………………………………………….(5)
We know that \[\sin \theta =\dfrac{Perpendicular}{Hypotenuse}\] …………………………………………………(6)
From equation (4), equation (5), and equation (6), we get
\[\Rightarrow \sin \theta =\dfrac{QD}{b}\]
 ……………………………………..(7)
We can see that the lines PR and BC are parallel to each other and we also know the property that the corresponding angles are equal to each other.
Using this property, we get
\[\angle ACB=\angle ARP\] ………………………………………….(8)
Now, from equation (1) and equation (8), we get
\[\angle ARP=\alpha \] ……………………………………………..(9)
We also know the property that in any triangle, the sum of the interior two angles is equal to the corresponding exterior angle.
Using this property in \[\Delta AQR\] , we get
\[\Rightarrow \angle ARP+\angle QAR=\angle AQP\] ………………………………………..(10)
Now, from equation (2) and equation (9), and equation (10), we get
\[\Rightarrow \alpha +\angle QAR=\gamma \]
\[\Rightarrow \angle QAR=\gamma -\alpha \] …………………………………………..(11)
Also, from the figure, we can say that \[\angle ACQ=\angle ACB-\angle QCD=\alpha -\beta \] and \[\angle QAR=\angle QAC\]………………………………..(12)
We know the sine formula for a triangle, \[\dfrac{a}{\sin A}=\dfrac{b}{\sin B}=\dfrac{c}{\sin C}\] …………………………………………..(13)
Now, applying the sine formula for \[\Delta AQC\] , we get
\[\dfrac{b}{\sin \angle QAC}=\dfrac{AQ}{\sin \angle ACQ}\] ………………………………………..(14)
From equation (11), equation (12), and equation (14), we get
\[\Rightarrow \dfrac{b}{\sin \left( \gamma -\alpha \right)}=\dfrac{AQ}{\sin \left( \alpha -\beta \right)}\]
\[\Rightarrow \dfrac{b\sin \left( \alpha -\beta \right)}{\sin \left( \gamma -\alpha \right)}=AQ\] ………………………………………….(15)
Now, in \[\Delta APQ\] , we have
\[\angle APQ=90{}^\circ \]
\[\angle AQP=\gamma \] ………………………………………………(16)
 Perpendicular = AP ………………………………………(17)
Hypotenuse = AQ ……………………………………….(18)
From equation (6), equation (16), equation (17), and equation (18), we get
\[\Rightarrow \sin \gamma =\dfrac{AP}{AQ}\]
\[\Rightarrow AQ\sin \gamma =AP\] ………………………………………..(19)
Now, from equation (15) and equation (19), we get
\[\Rightarrow \dfrac{b\sin \left( \alpha -\beta \right)}{\sin \left( \gamma -\alpha \right)}\sin \gamma =AP\] …………………………………………………(20)
Now, in \[\Delta APQ\] , we have
\[\angle QDC=90{}^\circ \]
\[\angle QCD=\beta \] ………………………………………………(21)
 Perpendicular = QD ………………………………………(22)
Hypotenuse = QC = \[b\] ……………………………………….(23)
From equation (6), equation (21), equation (22), and equation (23), we get
\[\Rightarrow \sin \beta =\dfrac{QD}{b}\]
\[\Rightarrow b\sin \beta =QD\] ………………………………………………..(24)
Now, from the figure, we can see that, QD = PB and \[AB=AP+PB\] ………………………………………(25)
From equation (20), equation (24), and equation (25), we have
\[\begin{align}
  & \Rightarrow AB=AP+PB \\
 & \Rightarrow AB=\dfrac{b\sin \alpha }{\sin \left( \gamma -\alpha \right)}\left[ \sin \left( \alpha -\beta \right)\sin \left( \gamma -\alpha \right)\sin \gamma +\sin \beta \sin \left( \gamma -\alpha \right) \right] \\
 & \Rightarrow AB=\dfrac{b\sin \alpha }{\sin \left( \gamma -\alpha \right)}\left[ \sin \gamma \cos \beta -\sin \beta \cos \gamma \right] \\
\end{align}\]
\[\Rightarrow AB=\dfrac{b\sin \alpha \sin \left( \gamma -\beta \right)}{\sin \left( \gamma -\alpha \right)}\] ………………………………….(26)
Therefore, the height of the hill is \[\dfrac{b\sin \alpha \sin \left( \gamma -\beta \right)}{\sin \left( \gamma -\alpha \right)}\] .
Hence, the correct option is (A).

Note: Whenever this type of question appears, always proceed with an appropriate diagram because even a small error in the diagram may result in the wrong solution. Therefore, be careful while drawing the diagram and make sure that the diagram represents the correct information as provided in the question.