Question

The angle of elevation of the top of the tower at a distance of 300 meters from its foot on a horizontal plane is found to be \[{30^ \circ }\]. The height of the tower is
A. 173m
B. \[300\sqrt 3 m\]
C. 100m
D. None of these

Answer 1

Hint: This problem is from heights and distances. We will easily solve this just by applying \[{30^ \circ } - {60^ \circ } - {90^ \circ }\] triangle theorem. That is side opposite to \[{60^ \circ }\] is \[{{{\sqrt 3 }} \!{\left/
 {\vphantom {{\sqrt 3 } 2}}\right.}
\!\lower0.7ex{2}}\] times the hypotenuse and that opposite to \[{30^ \circ }\] is half of the hypotenuse. This is the simple and correct approach we will use here only because we know the angle of elevation.

Step by step solution:
Now let’s draw the figure first with a tower of height supposed to say h and the angle of elevation is \[{30^ \circ }\]. Also given that the distance is 300 meters from its foot on a horizontal plane.

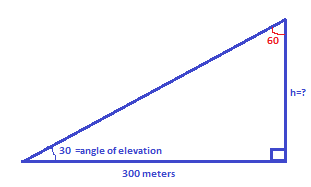
This is the figure so formed. Now we will find the height of the tower with the help of hypotenuse of the figure.
Using our \[{30^ \circ } - {60^ \circ } - {90^ \circ }\] triangle theorem,
Side opposite to \[{60^ \circ }\]=300
\[ \Rightarrow {{{\sqrt 3 }} \!{\left/
 {\vphantom {{\sqrt 3 } 2}}\right.}
\!\lower0.7ex{2}} \times hypt = 300\]
Thus value of hypotenuse is
\[ \Rightarrow hypt = 300 \times {{2} \!{\left/
 {\vphantom {2 {\sqrt 3 }}}\right.}
\!\lower0.7ex{{\sqrt 3 }}}\]
Thus we get, \[ \Rightarrow hypt = {{{600}} \!{\left/
 {\vphantom {{600} {\sqrt 3 }}}\right.}
\!\lower0.7ex{{\sqrt 3 }}}m\]
Now to get the height of the tower we will use this hypotenuse length.
Height of the tower is exactly the side opposite to the elevation angle \[{30^ \circ }\].
Side opposite to \[{30^ \circ }\]= \[{{1} \!{\left/
 {\vphantom {1 2}}\right.}
\!\lower0.7ex{2}} \times hypt\]
\[ \Rightarrow h = {{1} \!{\left/
 {\vphantom {1 2}}\right.}
\!\lower0.7ex{2}} \times hypt\]
Putting the value of hypotenuse
\[ \Rightarrow h = {{1} \!{\left/
 {\vphantom {1 2}}\right.}
\!\lower0.7ex{2}} \times {{{600}} \!{\left/
 {\vphantom {{600} {\sqrt 3 }}}\right.}
\!\lower0.7ex{{\sqrt 3 }}}\]
\[ \Rightarrow h = {{{300}} \!{\left/
 {\vphantom {{300} {\sqrt 3 }}}\right.}
\!\lower0.7ex{{\sqrt 3 }}}m\]
This is the height of the tower \[ \Rightarrow h = {{{300}} \!{\left/
 {\vphantom {{300} {\sqrt 3 }}}\right.}
\!\lower0.7ex{{\sqrt 3 }}}m\]

But there is no option matching here. Thus option D is the correct option “none of these”.

Note:
Students don’t hurry when you choose options because most of the students find the correct answer but fail to select. See here in this case the answer is in ratio form but since option B is similar looking people may tick it as correct. But it is the wrong one. So be careful when you choose the option.