Question

The angle which the velocity vector of a projectile, thrown with a velocity v at an angle θ to the horizontal, will make with the horizontal after time t of its being thrown up is
A. $\theta $
B. ${\tan ^{ - 1}}\left( {\dfrac{\theta }{t}} \right)$
C. ${\tan ^{ - 1}}\left( {\dfrac{{v\cos \theta }}{{v\sin \theta - gt}}} \right)$
D. ${\tan ^{ - 1}}\left( {\dfrac{{v\sin \theta - gt}}{{v\cos \theta }}} \right)$

Answer 1

Hint: This is the case of projectile motion where the particle is projected with some angle to the horizontal. The acceleration acting on the projectile is only in vertical direction because gravity will be acting only in vertical direction and along horizontal direction there is no force. We will find out the velocity along x and y directions after time ‘t’ to solve this.

Formula used:
 $\eqalign{
  & {v_x} = v(\cos \theta ) \cr
  & {v_y} = v(\sin \theta ) - gt \cr} $

Complete step by step answer:
When a particle is projected with some angle to the horizontal then that particle will have both horizontal displacement and vertical displacement. Since there will be no force along the horizontal direction the velocity along the horizontal direction will be the same throughout its motion while there is force along the vertical direction so velocity along vertical direction will vary.
After the time ‘t’ let the velocity be ‘v’ and we will resolve this velocity along x and y directions.
Along x direction velocity component will be
${v_x} = v(\cos \theta )$
Along y direction velocity component will be
${v_y} = v(\sin \theta ) - gt$
Where $\theta $ is the angle made by the initial velocity vector with horizontal and ‘v’ is the initial velocity and ‘g’ is the acceleration due to gravity in downward direction, so there is a negative sign in the formula.

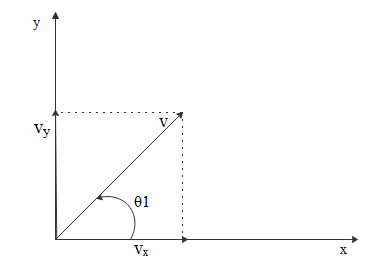
The above figure represents the condition of the projectile after time ‘t’ and the angle made by the velocity vector with the horizontal.
After time ‘t’ let the velocity vector is making $\theta_ 1$ angle with the horizontal then we have
$\eqalign{
  & \tan (\theta_1) = \dfrac{{{v_y}}}{{{v_x}}} \cr
  & \Rightarrow \tan (\theta_1) = \dfrac{{v(\sin \theta ) - gt}}{{v(\cos \theta )}} \cr
  & \Rightarrow \theta_1 = {\tan ^{ - 1}}\left( {\dfrac{{v(\sin \theta ) - gt}}{{v(\cos \theta )}}} \right) \cr} $

So, the correct answer is “Option D”.

Note: Since force is acting along the vertical direction the velocity in vertical direction will change. These equations are valid only if acceleration is constant and doesn’t vary with time. If it varies then we have to integrate to find out the velocity.