
The angular spread of central maximum, in diffraction pattern, does not depend on _____________
A) The distance between the slit and the source
B) Width of the slit
C) Wavelength of light
D) Frequency of light
Answer
507k+ views
Hint: This problem can be solved by writing the formula for the path difference for the central maximum in single slit diffraction and then obtaining the formula for the angular width of the central maximum for it. Upon analysis of this formula, we can check upon which factor the angular width does not depend upon.
Formula used:
Complete step-by-step answer:
Let us try to get the mathematical formula for the angular width of the central maximum in single slit diffraction.
The path difference
Where
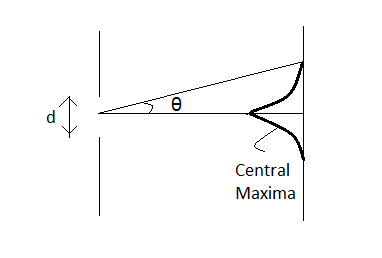
Also, the path difference
where
Comparing (1) and (2), we get,
Now, as is clear from the figure, the central maximum is symmetric on both sides of the central axis. Hence, the angular width
Hence, we can see that the angular width of the central maximum does not depend on the distance between the slit and the source. Hence, the correct option is A) The distance between the slit and the source.
Note: Students might be tempted to think that the frequency of the light can also be the correct answer in this question as it has no mention in equation (4). However, they must remember that the wavelength and frequency of light are related to each other as their product is a constant (the speed of light) and hence, frequency is inversely proportional to the wavelength of light. Therefore, the angular width of the central maximum depends upon the frequency of the light (since it depends upon the wavelength).
Formula used:
Complete step-by-step answer:
Let us try to get the mathematical formula for the angular width of the central maximum in single slit diffraction.
The path difference
Where

Also, the path difference
where
Comparing (1) and (2), we get,
Now, as is clear from the figure, the central maximum is symmetric on both sides of the central axis. Hence, the angular width
Hence, we can see that the angular width of the central maximum does not depend on the distance between the slit and the source. Hence, the correct option is A) The distance between the slit and the source.
Note: Students might be tempted to think that the frequency of the light can also be the correct answer in this question as it has no mention in equation (4). However, they must remember that the wavelength and frequency of light are related to each other as their product is a constant (the speed of light) and hence, frequency is inversely proportional to the wavelength of light. Therefore, the angular width of the central maximum depends upon the frequency of the light (since it depends upon the wavelength).
Recently Updated Pages
Master Class 12 Economics: Engaging Questions & Answers for Success

Master Class 12 Maths: Engaging Questions & Answers for Success

Master Class 12 Biology: Engaging Questions & Answers for Success

Master Class 12 Physics: Engaging Questions & Answers for Success

Master Class 4 Maths: Engaging Questions & Answers for Success

Master Class 4 English: Engaging Questions & Answers for Success

Trending doubts
Give 10 examples of unisexual and bisexual flowers

Draw a labelled sketch of the human eye class 12 physics CBSE

a Tabulate the differences in the characteristics of class 12 chemistry CBSE

Differentiate between homogeneous and heterogeneous class 12 chemistry CBSE

Why is the cell called the structural and functional class 12 biology CBSE

Differentiate between insitu conservation and exsitu class 12 biology CBSE




