Question

The aperture diameter of a telescope is 5 m. The separation between the moon and the earth is $ 4 \times {10^5}{\text{ km}} $ . With light of wavelength of $ 5500A^\circ $ , what is the minimum separation between objects on the surface of the moon so that they are just resolved?
A. 60 m
B. 20 m
C. 600 m
D. 200 m

Answer 1

Hint: The Rayleigh criterion is used to define the limit of resolution between two distant objects. It is also known as the resolving power and gives the smallest distance up to which all the details of an object can be clearly seen.

Formula used: $ \theta = \dfrac{{1.22\lambda }}{D} $ where, $ \theta $ is the minimum angle of separation between two objects, $ \lambda $ is the wavelength of visible light and $ D $ is the diameter of the lens.

Complete step by step solution:
In the question, we are provided with the following data about the telescope which is used for observing the two points on the moon:
Aperture diameter of the telescope is $ D = 5m $ .
Distance between the Earth and the moon is $ d = 4 \times {10^5}{\text{ km}} = 4 \times {10^8}{\text{ m}} $ . $ [\because 1{\text{km}} = 1000{\text{m}}] $
Wavelength of light is $ \lambda = 5500{A^\circ } = 5500 \times {10^{ - 10}}m $ .
We must remember to convert all the units into meters. We know that the limit of resolution between two points is given as:
 $ \theta = \dfrac{{1.22\lambda }}{D} $ ......[Eq. 1]
But this resolution is defined in terms of the angular separation, while we are required to find the distance. Hence, we convert this into linear distance as:
 $ \theta = \dfrac{s}{d} $
where $ s $ is the distance between the points

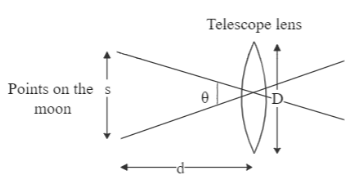
Putting this value in Eq. 1, gives us:
 $ \theta = \dfrac{s}{d} = \dfrac{{1.22\lambda }}{D} $
Solving for $ s $ , we get:
 $ s = \dfrac{{1.22\lambda \times d}}{D} $
Putting the values of wavelength, aperture and distance:
 $ s = \dfrac{{1.22 \times 5500 \times {{10}^{ - 10}} \times 4 \times {{10}^8}}}{5} $ [Exponents in the power of 10 add up]
 $ s = \dfrac{{26840 \times {{10}^{ - 2}}}}{5} = 53.68m $
 $ \therefore $ The minimum separation between the two points on the moon is $ 53.68m $ which is approximately equal to 60 m.
Hence, the answer is option A.

Note:
The limit of resolution for a healthy human eye is about $ 0.2mm $ . This means any objects closer than this distance would require us to use an external aid. Similarly in the question above, the 60 m limit implies we would be able to see all the objects that are separated by a distance greater than this. Anything closer would have blurred outlines with the telescope provided.