Question

The apparent weight of the body in a liquid is
A) $V\left( {\rho - {\rho _L}} \right)g$
B) $V\rho g$
C) $V{\rho _L}g$
D) None of these.

Answer 1

Hint:Whenever a body is submerged partially or fully in a liquid it experiences an upthrust. The weight of the body is felt to decrease under the action of the upthrust. Archimedes’ principle gives the apparent weight of the body to be equal to the difference between the weight of the body and the upthrust experienced by it.

Formulas used:
-The apparent weight of a body in a liquid is given by, ${W_{apparent}} = W - {F_b}$ where $W$ is the weight of the body and ${F_b}$ is the force of buoyancy or upthrust experienced by the body.
-The weight of a body is given by, $W = V\rho g$ where $V$ is the volume of the body, $\rho $ is the density of the body and $g$ is the acceleration due to gravity.
-The upthrust on a body by a liquid is given by, ${F_b} = V{\rho _L}g$ where $V$ is the volume of the displaced liquid, ${\rho _L}$ is the density of the liquid and $g$ is the acceleration due to gravity.

Complete step by step answer.
Step 1: Sketch a figure representing a body in liquid.
     

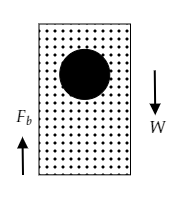
The above figure depicts a body immersed in some liquid. (It can be partially or fully immersed)
The force of buoyancy or upthrust ${F_b}$ is directed upwards and the weight of the body $W$ is directed downwards.
Let $V$ be the volume and $\rho $ be the density of the body and ${\rho _L}$ be the density of the liquid.

Step 2: Based on Archimedes’ principle, express the apparent weight of the body.
The weight of the body can be expressed as $W = V\rho g$ ----------- (1).
The upthrust experienced by the body can be expressed as ${F_b} = V{\rho _L}g$ --------- (2).
According to Archimedes’ principle, the upthrust acting on the body will be equal to the weight of the body. So the difference between the weight and the upthrust will correspond to the apparent weight of the body.
i.e., ${W_{apparent}} = W - {F_b}$ ------ (3)
Substituting equations (1) and (2) in (3) we get, ${W_{apparent}} = V\rho g - V{\rho _L}g$
$ \Rightarrow {W_{apparent}} = V\left( {\rho - {\rho _L}} \right)g$

So the correct option is A.

Note: The volume of the liquid displaced on immersing the body will be equal to the volume of the body. The mass of an object is expressed as $m = V\rho $ where $V$ is the volume of the object and $\rho $ is its density. Since the weight of an object is usually expressed as $W = mg$ , substituting $m = V\rho $ in the relation for the weight we get, $W = V\rho g$ as equation (1).