Question

The area bounded by \[y = 2 - |2 - x|\] and \[y = \dfrac{3}{{|x|}}\] is:
A) $\dfrac{{4 + 3\ln 3}}{2}$
B) $\dfrac{{4 - 3\ln 3}}{2}$
C) $\dfrac{3}{2} + \ln 3$
D)$\dfrac{1}{2} + \ln 3$

Answer 1

Hint: The most general class of problems in calculating the area of bounded regions is the one involving the regions between two curves. All other problems can be treated as a subset. Besides being an important application of definite integrals, these problems also give one an idea about the nature of the two curves involved. The area under a curve between two points can be found by doing a definite integral between the two points.

 Complete step-by-step solution
The two curves given includes the modulus in them so, the function can be bifurcated into two different functions at the critical point as:
$y = 2 - |2 - x| \to \left\{
  x;x < 2 \\
  4 - x,x > 2 \\
  \right.$
Similarly,
$y = \dfrac{3}{{|x|}} \to \left\{
  \dfrac{3}{x},x > 0 \\
   - \dfrac{3}{x},x < 0 \\
  \right.$

The rough sketch for the two curves is drawn as:

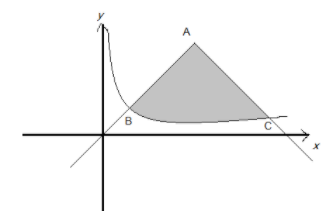
Now, we need to determine the common points to the curves, which is the point of intersection of the two curves. So, solving the two equations by equating the two functions as:
Case 1
 $
   \Rightarrow\dfrac{3}{x} = 2 - 2 + x \\
 \Rightarrow 3 = {x^2} \\
 \Rightarrow x = \sqrt 3 \\
 $
For, $x = \sqrt 3 $ the value $y$ is calculated by substituting the value of $x = \sqrt 3 $ as:

$
  y = \dfrac{3}{x} \\
   = \dfrac{3}{{\sqrt 3 }} = \sqrt 3 \\
 $
Again,

Case 2
$
 \Rightarrow \dfrac{3}{x} = 2 + 2 - x \\
 \Rightarrow 3 = 4x - {x^2} \\
 \Rightarrow {x^2} - 4x + 3 = 0 - - - - (i) \\
 $
Splitting the middle term of equation (i) for the value of x as:
$
 \Rightarrow {x^2} - 3x - x + 3 = 0 \\
 \Rightarrow x(x - 3) - 1(x - 3) = 0 \\
 \Rightarrow (x - 1)(x - 3) = 0 \\
  x = 1;3 \\
 $
Here, $x = 1$ it is not possible as $x = \sqrt 3 $ it has already been a point of intersection. So, $x = 3$ is another point of intersection for which the value $y$ is calculated as:
$
  y = \dfrac{3}{x} \\
   = \dfrac{3}{3} = 1 \\
 $
Hence, the two-point of the intersection of the curves are $B\left( {\sqrt 3 ,\sqrt 3 } \right)$ and $C\left( {3,1} \right)$.
Now, to determine the area under the curves, we need to integrate equations from $x = \sqrt 3 $ to $x = 3$. As 2 is one of the critical points so, we have to bifurcate our calculation in two integrals as:

\[
  A = \int\limits_{\sqrt 3 }^3 {({y_1} + {y_2})dx} \\
   = \int\limits_{\sqrt 3 }^2 {({y_1} - {y_2})dx} + \int\limits_2^3 {({y_1} - {y_2})dx} \\
   = \int\limits_{\sqrt 3 }^2 {\left( {x - \dfrac{3}{x}} \right)dx} + \int\limits_2^3 {\left( {4 - x - \dfrac{3}{x}} \right)} dx \\
   = \left[ {\dfrac{{{x^2}}}{2} - 3\ln x} \right]_{\sqrt 3 }^2 + \left[ {4x - \dfrac{{{x^2}}}{2} - 3\ln x} \right]_2^3 \\
 \]
Now, substituting the integral limits, we get:
\[
  A = \left( {\dfrac{4}{2} - 3\ln 2} \right) - \left( {\dfrac{3}{2} - 3\ln \sqrt 3 } \right) + \left( {12 - \dfrac{9}{2} - 3\ln 3} \right) - \left( {8 - 2 - 3\ln 2} \right) \\
   = 2 - 3\ln 2 - 1.5 + 1.5\ln 3 + 12 - 4.5 - 3\ln 3 - 8 + 2 + 3\ln 2 \\
   = \left( {2 - 1.5 + 12 - 4.5 - 8 + 2} \right) + \left( { - 3\ln 2 + 1.5\ln 3 - 3\ln 3 - 3\ln 2} \right) \\
   = 2 - 1.5\ln 3 \\
   = \dfrac{{4 - 3\ln 3}}{2} \\
 \]
Hence, the area bounded by \[y = 2 - |2 - x|\] and \[y = \dfrac{3}{{|x|}}\] is \[\dfrac{{4 - 3\ln 3}}{2}\]

Thus the correct answer is option B.

Note:The second function is not defined at \[x = 0\]. Therefore, any bounded region will either be complete to the left of the y-axis or completely to the right of the y-axis. To find the area under the curve y = f(x) between x = a and x = b, integrate y = f(x) between the limits of a and b. Areas under the x-axis will come out negative, and areas above the x-axis will be positive. If plotting one of the curves is notoriously difficult, one can get the idea of the nature of the curve by calculating the area of the region bounded by the curve with some other known curve.