
Answer
470.7k+ views
Hint: We have two lines as \[4x + 3y = 15\]and \[4x + 3y = 15\]. We can see both lines are parallel altogether. So using the formula for distance between two parallel lines, which is the perpendicular distance between two parallel lines, \[ax + by + c = 0\]and \[ax + by + d = 0\]is denoted by, \[\dfrac{{\left| {{\text{c - d}}} \right|}}{{\sqrt {{{\text{a}}^{\text{2}}}{\text{ + }}{{\text{b}}^{\text{2}}}} }}\]units, we’ll find the diameter of the circle resulting in the radius. So, using the radius we’ll find the area of the circle using the formula of area of the circle which is \[{\text{$\pi$ (radius}}{{\text{)}}^{\text{2}}}\], and then comparing it with the given area of circle, we find the value of m.
Complete step by step Answer:
Here, We have two lines as \[4x + 3y = 15\]and \[4x + 3y = 15\].
And it is clear that they are parallel.
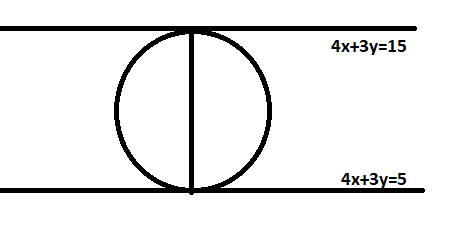
Since both lines are parallel, (visible from the image)
So, we will have the Diameter=the perpendicular distance between two lines,
Now the perpendicular distance between two lines, \[ax + by + c = 0\]and \[ax + by + d = 0\]is denoted by,
\[\dfrac{{\left| {{\text{c - d}}} \right|}}{{\sqrt {{{\text{a}}^{\text{2}}}{\text{ + }}{{\text{b}}^{\text{2}}}} }}\]units
So, we have here, \[{\text{a = 4, b = 3, c = - 15,d = - 5,}}\]
The perpendicular distance would be,
\[\dfrac{{\left| {{\text{ - 15 - ( - 5)}}} \right|}}{{\sqrt {{\text{16 + 9}}} }}\]units
\[{\text{ = }}\dfrac{{{\text{10}}}}{{\text{5}}}{\text{ = 2units}}\]
So, Diameter is 2 units,
Now, the radius is, \[\dfrac{{\text{D}}}{{\text{2}}}{\text{ = }}\dfrac{{\text{2}}}{{\text{2}}}{\text{ = 1}}\]units,
We are finding the area now, so, area= \[{\text{$\pi$ (radius}}{{\text{)}}^{\text{2}}}\]=\[{\text{$\pi$ (1}}{{\text{)}}^{\text{2}}}\]\[{\text{ = $\pi$ }}\]units
So, we have, \[{\text{m$\pi$ = $\pi$ }}\]
So, \[{\text{m = 1}}\].
Note: The perpendicular distance formula of the lines is used here. We see the perpendicular distance between two lines, \[ax + by + c = 0\]and \[ax + by + d = 0\]is denoted by,
\[\dfrac{{\left| {{\text{c - d}}} \right|}}{{\sqrt {{{\text{a}}^{\text{2}}}{\text{ + }}{{\text{b}}^{\text{2}}}} }}\]units.
We can also find the distance between two lines by taking any point on one line and then by using the formula for a point from a line i.e.
Let the point be (l,m) and equation of line be ax+by+c=0
The distance between them\[\dfrac{{\left| {{\text{lx + bm + c}}} \right|}}{{\sqrt {{{\text{a}}^{\text{2}}}{\text{ + }}{{\text{b}}^{\text{2}}}} }}\]
After finding the diameter you should not forget to find its radius first and then the area, otherwise, the answer would be wrong.
Complete step by step Answer:
Here, We have two lines as \[4x + 3y = 15\]and \[4x + 3y = 15\].
And it is clear that they are parallel.

Since both lines are parallel, (visible from the image)
So, we will have the Diameter=the perpendicular distance between two lines,
Now the perpendicular distance between two lines, \[ax + by + c = 0\]and \[ax + by + d = 0\]is denoted by,
\[\dfrac{{\left| {{\text{c - d}}} \right|}}{{\sqrt {{{\text{a}}^{\text{2}}}{\text{ + }}{{\text{b}}^{\text{2}}}} }}\]units
So, we have here, \[{\text{a = 4, b = 3, c = - 15,d = - 5,}}\]
The perpendicular distance would be,
\[\dfrac{{\left| {{\text{ - 15 - ( - 5)}}} \right|}}{{\sqrt {{\text{16 + 9}}} }}\]units
\[{\text{ = }}\dfrac{{{\text{10}}}}{{\text{5}}}{\text{ = 2units}}\]
So, Diameter is 2 units,
Now, the radius is, \[\dfrac{{\text{D}}}{{\text{2}}}{\text{ = }}\dfrac{{\text{2}}}{{\text{2}}}{\text{ = 1}}\]units,
We are finding the area now, so, area= \[{\text{$\pi$ (radius}}{{\text{)}}^{\text{2}}}\]=\[{\text{$\pi$ (1}}{{\text{)}}^{\text{2}}}\]\[{\text{ = $\pi$ }}\]units
So, we have, \[{\text{m$\pi$ = $\pi$ }}\]
So, \[{\text{m = 1}}\].
Note: The perpendicular distance formula of the lines is used here. We see the perpendicular distance between two lines, \[ax + by + c = 0\]and \[ax + by + d = 0\]is denoted by,
\[\dfrac{{\left| {{\text{c - d}}} \right|}}{{\sqrt {{{\text{a}}^{\text{2}}}{\text{ + }}{{\text{b}}^{\text{2}}}} }}\]units.
We can also find the distance between two lines by taking any point on one line and then by using the formula for a point from a line i.e.
Let the point be (l,m) and equation of line be ax+by+c=0
The distance between them\[\dfrac{{\left| {{\text{lx + bm + c}}} \right|}}{{\sqrt {{{\text{a}}^{\text{2}}}{\text{ + }}{{\text{b}}^{\text{2}}}} }}\]
After finding the diameter you should not forget to find its radius first and then the area, otherwise, the answer would be wrong.
Recently Updated Pages
How is abiogenesis theory disproved experimentally class 12 biology CBSE

What is Biological Magnification

Explain the Basics of Computer and Number System?

Class 11 Question and Answer - Your Ultimate Solutions Guide

Write the IUPAC name of the given compound class 11 chemistry CBSE

Write the IUPAC name of the given compound class 11 chemistry CBSE

Trending doubts
Who was the Governor general of India at the time of class 11 social science CBSE

Difference between Prokaryotic cell and Eukaryotic class 11 biology CBSE

Define the term system surroundings open system closed class 11 chemistry CBSE

State and prove Bernoullis theorem class 11 physics CBSE

Proton was discovered by A Thomson B Rutherford C Chadwick class 11 chemistry CBSE

What organs are located on the left side of your body class 11 biology CBSE




