Question

The area of the plane region bounded by the curve $0{\text{ }}to{\text{ }}a.$ ${\mathbf{x}} + {\mathbf{2}}{{\mathbf{y}}^2}{\text{ }} = {\text{ }}{\mathbf{0}}$ and ${\mathbf{x}} + {\mathbf{3}}{{\mathbf{y}}^2}{\text{ }} = {\mathbf{1}}$ is equal to:
A. $ - {\mathbf{4}}/{\mathbf{3}}$
B. ${\mathbf{4}}/{\mathbf{3}}$
C. ${\mathbf{2}}/{\mathbf{3}}$
D. None of these

Answer 1

Hint:As the given equations are:
${\mathbf{x}} + {\mathbf{2}}{{\mathbf{y}}^2}{\text{ }} = {\text{ }}{\mathbf{0}}$ and ${\mathbf{x}} + {\mathbf{3}}{{\mathbf{y}}^2}{\text{ }} = {\mathbf{1}}$
And we know that the curve, having two variables in which the degree of one variable is $2$ and the other one is$1$, are of the parabola.So, to find the area of the plane region covered by these two given parabolas, we need to find the points of intersections and then need to apply integration within limits.

Complete step by step answer:
The given curves are: ${\mathbf{x}} + {\mathbf{2}}{{\mathbf{y}}^2}{\text{ }} = {\text{ }}{\mathbf{0}}$ and ${\mathbf{x}} + {\mathbf{3}}{{\mathbf{y}}^2}{\text{ }} = {\mathbf{1}}$

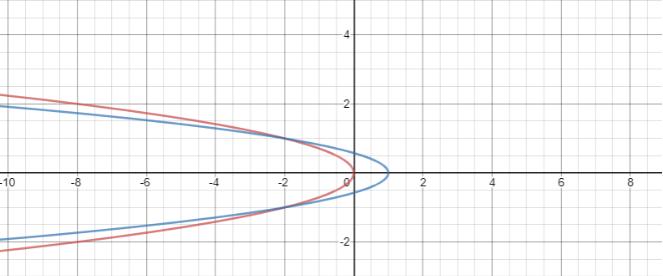
In the case of the first curve:
${\mathbf{x}} + {\mathbf{2}}{{\mathbf{y}}^2}{\text{ }} = {\text{ }}{\mathbf{0}}$
i.e. ${\mathbf{x}} = - {\mathbf{2}}{{\mathbf{y}}^2}$
i.e. $\dfrac{{ - x}}{2} = {{\mathbf{y}}^2}$
This is the equation of left-handed parabola having the vertex $\left( {0,0} \right).$
In case of second parabola:
This is also the equation of parabola.
So, to find the area between the parabolas, we just need to find the area points of intersection of these two curves.
As we know: ${{\mathbf{y}}^2} = {{\mathbf{y}}^2}$
putting different values of on both the sides:
i.e. $\dfrac{{ - x}}{2} = \dfrac{{1 - x}}{3}$

solving and arranging the terms:
i.e. $ - 3x + 2x = 2$
$x = - 2$
Therefore, putting the value of in the equation of first curve i.e ${y^2} = \dfrac{{ - x}}{2}$
it becomes, ${y^2} = \dfrac{{ - ( - 2)}}{2} = 1$
i.e. ${y^2} = \dfrac{{ - ( - 2)}}{2} = 1$
i.e. ${y^{{2^{}}}} = 1$ ${y^2} = 1$
$y = 1, - 1$
Hence, there are two points of intersection $\left( { - 2, - 1} \right){\text{ }}and{\text{ }}\left( { - 2,1} \right)$

Now, to find the required area, we are going to integrate the curve equation w.r.t y taking limits from $\_1{\text{ }}to{\text{ }}1$.
Hence, required area:
$|\int\limits_{ - 1}^1 {\left( {x + 3{y^2} - 1} \right)dy|} $
Putting the value of x from first curve I;
$|\int\limits_{ - 1}^1 {\left( {x + 3{y^2} - 1} \right)dy|} $
$\Rightarrow|\int\limits_{ - 1}^1 {\left( { - 2{y^2} + 3{y^2} - 1} \right)dy|} $
$\Rightarrow |\int\limits_{ - 1}^1 {\left( {{y^2} - 1} \right)dy|} $
We also know that by doubling the integrand if the limits are $-a{\text{ }}to{\text{ }}a$, we can change it to $0{\text{ }}to{\text{ }}a.$
Therefore, Required area $ = 2|\int\limits_0^1 {\left( {{y^2} - 1} \right)dy|} $
$\Rightarrow 2\left( {\dfrac{{{y^3}}}{3} - y} \right)_0^1$
$\Rightarrow 2\left( {\left( {\dfrac{1}{3} - 1} \right) - \left( {\dfrac{0}{3} - 0} \right)} \right)_0^1$
$\Rightarrow 2| - \dfrac{2}{3}|$
Solving the modulus; $ = \dfrac{4}{3}$ square units

Note: Parabola is one of the important curves in mathematics. There are major four types of parabola i.e:
a. Upward Parabola represented by equation: $\int\limits_a^b {kdt} = \left[ {kt} \right]_a^b = kb - ka = k(b - a)$ ${(x - h)^2} = 4p(y - k)$
b. Downward parabola represented by equation: ${(x - h)^2} = - 4p(y - k)$
c. Left handed parabola represented by equation: ${(y - k)^2} = - 4p(x - h)$
d. Right handed parabola represented by equation: ${(y - k)^2} = 4p(x - h)$
having vertex (h,k)
To find the area of the plane region covered by two curves, we usually use integration within the limits of any variable.So, in this equation we did integration with respect to y and put the value of x in the form of y in the second curve from the first curve to form the integrand and the limits were of y. The formulae used in this problem are:
$\int\limits_a^b {{t^n}dt} = \left[ {\dfrac{{{t^{n + 1}}}}{{n + 1}}} \right]_a^b = \dfrac{{{b^{n + 1}}}}{{n + 1}} - \dfrac{{{a^{n + 1}}}}{{n + 1}}$
and $\int\limits_a^b {kdt} = \left[ {kt} \right]_a^b = kb - ka = k(b - a)$
Hence, by doing all these calculations, the correct option is ‘B’ i.e $4/3$square units.