Question

The area of the rectangle is $5\dfrac{4}{5}$ square meters. The width of the rectangle is $2\dfrac{1}{4}$ meter. How long is the rectangle?

Answer 1

Hint: Here we have to find the length of a rectangle whose area and width is given. Firstly we will convert the mixed fractions value given in improper fraction. Then we will write the formula for finding the area of a rectangle and substitute the values in it. Finally we will simplify the equation and get our desired answer.


Complete step by step answer:
We have been given the information of the rectangle as follows:
Area of rectangle $=5\dfrac{4}{5}\,{{m}^{2}}$…..$\left( 1 \right)$
Width of rectangle $=2\dfrac{1}{4}\,m$…..$\left( 2 \right)$
Now firstly we will convert the values from mixed fraction to improper fraction by using the formula given below:
$a\dfrac{b}{c}=\dfrac{\left( a\times c \right)+b}{c}$
Using the formula above in equation (1) we get,
Area of rectangle $=\dfrac{\left( 5\times 5 \right)+4}{5}\,{{m}^{2}}$
Area of rectangle $=\dfrac{29}{5}\,{{m}^{2}}$….$\left( 3 \right)$
Using the formula in equation (2) we get,
Width of rectangle $=\dfrac{\left( 2\times 4 \right)+1}{4}\,m$
Width of rectangle $\dfrac{9}{4}\,m$….$\left( 4 \right)$
So we can draw the rectangle as follows:

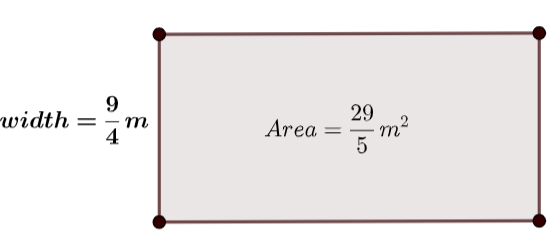
Next we know the area of rectangle is calculated as follows:
Area $=$ Length $\times $ Width
Substitute the value from equation (3) and (4) above and let Length $=l$ ,
$\Rightarrow \dfrac{29}{5}\,{{m}^{2}}=l\times \dfrac{9}{4}\,m$
Keep $l$ on one side and take the rest value on another side as follows:
$\Rightarrow l=\dfrac{\dfrac{29}{5}\,{{m}^{2}}}{\dfrac{9}{4}\,m}$
$\Rightarrow l=\dfrac{29}{5}\times \dfrac{4}{9}\,{{m}^{2-1}}$
So we get,
$\Rightarrow l=\dfrac{116}{45}\,m$
On converting above value in mixed fraction we get,
$l=2\dfrac{26}{45}\,m$
We get the rectangle as

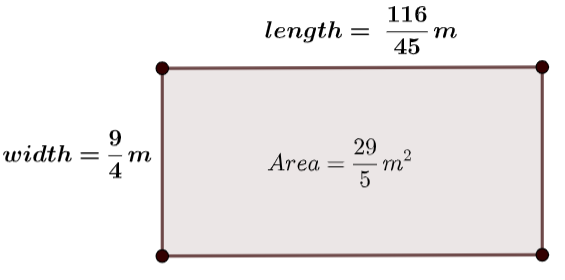
Hence a rectangle is $2\dfrac{26}{45}$ meter long.

Note: Rectangle is a four sided polygon whose opposite sides are equal in length and are always parallel to each other. The two sides at each corner form a ${{90}^{\circ }}$ (Right angle) . Area of a rectangle is equal to the product of its length and width. In this question converting the mixed fraction into improper fraction is an important step as it makes our calculation less complicated.